题目内容
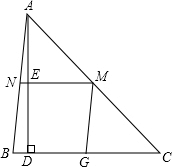
已知，如图，在△ABC中，AD平分∠BAC，点D是BC的中点，DM⊥AB，DN⊥AC，垂足分别为M、N，求证：BM=CN．考点：全等三角形的判定与性质,角平分线的性质
专题：证明题
分析：由AD为角平分线，且DM⊥AB，DN⊥AC，利用角平分线性质得到DM=DN，再由BD=CD，利用HL得到直角三角形BDM与直角三角形CDN全等，利用全等三角形的性质即可得证．
解答：证明：∵在△ABC中，AD平分∠BAC，DM⊥AB，DN⊥AC，
∴DM=DN，
∵D为BC的中点，
∴BD=CD，
在Rt△BDM和Rt△CDN中，
，
∴Rt△BDM≌Rt△CDN（HL），
∴BM=CN．
∴DM=DN，
∵D为BC的中点，
∴BD=CD，
在Rt△BDM和Rt△CDN中，
|
∴Rt△BDM≌Rt△CDN（HL），
∴BM=CN．
点评：此题考查了全等三角形的判定与性质，以及角平分线性质，熟练掌握全等三角形的判定与性质是解本题的关键．
练习册系列答案
相关题目
若关于x的二次三项式x2-mx+4是完全平方式，则（ ）
| A、m=4 | B、m=-4 |
| C、m=±4 | D、m=±2 |
如图所示，有一块锐角三角形的余料ABC，它的边BC=150mm，AB=100mm，要把它加工成菱形零件，使菱形的一边在BC上，其余的两个顶点分别在AB，AC上，加工成的菱形的高ED=51mm，求△ABC的高AD．