题目内容
1. 如图,在等边△ABC中,AD与BE相交于点P,∠DPE=120°,AB=8,BD=2,则AE=6.
如图,在等边△ABC中,AD与BE相交于点P,∠DPE=120°,AB=8,BD=2,则AE=6.
分析 由等边三角形的性质得出AC=AB=BC=8,∠ABD=∠BCE=60°,证出∠BAD=∠CBE,由ASA证明△ABD≌△BCE,得出BD=CE=2,即可得出AE的长.
解答 解:∵△ABC是等边三角形,
∴AC=AB=BC=8,∠ABD=∠BCE=60°,
∵∠DFE=120°,
∴∠APE=60°,
∵∠APE=∠BAD+∠ABP,∠ABD=∠CBE+∠ABP,
∴∠BAD=∠CBE,
在△ABD与△BCE中,$\left\{\begin{array}{l}{∠BAD=∠CBE}&{\;}\\{AB=BC}&{\;}\\{∠ABD=∠BCE}&{\;}\end{array}\right.$,
∴△ABD≌△BCE(ASA),
∴CE=BD=2,
∴AE=AC-CE=6,
故答案为:6
点评 本题考查了等边三角形的性质、全等三角形的判定与性质;熟练掌握等边三角形的性质,证明三角形全等是解决问题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
11.有某种规律的一列数:20+0.5,30+1,40+1.5…,其中第五个数是( )
| A. | 50+2 | B. | 60+2.5 | C. | 60+2 | D. | 70+3 |
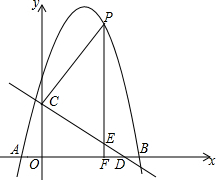 如图,抛物线y=-x2+bx+c与x轴交于点A(-1,0),B(5,0)两点,直线y=-$\frac{3}{4}$x+3与y轴交于点C,与x轴交于点D.点P是x轴上方的抛物线上一动点,过点P作PF⊥x轴于点F,交直线CD于点E.若点E′是点E关于直线PC的对称点,当点E′落在y轴上时,点P的坐标为(-$\frac{1}{2}$,$\frac{11}{4}$),(4,5),(3-$\sqrt{11}$,2$\sqrt{11}$-3).
如图,抛物线y=-x2+bx+c与x轴交于点A(-1,0),B(5,0)两点,直线y=-$\frac{3}{4}$x+3与y轴交于点C,与x轴交于点D.点P是x轴上方的抛物线上一动点,过点P作PF⊥x轴于点F,交直线CD于点E.若点E′是点E关于直线PC的对称点,当点E′落在y轴上时,点P的坐标为(-$\frac{1}{2}$,$\frac{11}{4}$),(4,5),(3-$\sqrt{11}$,2$\sqrt{11}$-3). 如图,B、C、F、E在同一直线上,AB、DE交于点G,DC=AF,∠B=∠E,∠D=∠A,
如图,B、C、F、E在同一直线上,AB、DE交于点G,DC=AF,∠B=∠E,∠D=∠A,