题目内容
19.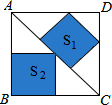 如图,边长为6的大正方形中有两个小正方形,若两个小正方形的面积分别为S1和S2,比较S1与S2的大小( )
如图,边长为6的大正方形中有两个小正方形,若两个小正方形的面积分别为S1和S2,比较S1与S2的大小( )| A. | S1>S2 | B. | S1<S2 | C. | S1=S2 | D. | 不能确定 |
分析 由图可得,S2的边长为3,由AH=$\sqrt{2}$HN,NH=HG=$\sqrt{2}$GD,可得AC=2HD,HD=2,HG=2$\sqrt{2}$;再分别算出S1、S2的面积,即可解答.
解答 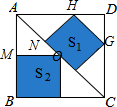 解:如图,
解:如图,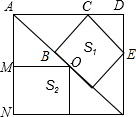
设正方形S1的边长为x,
∵△ANH和△HDG都为等腰直角三角形,
∴AN=NH,DH=DG,∠ANH=∠D=90°,
∴sin∠CAB=sin45°=$\frac{NH}{AH}$=$\frac{\sqrt{2}}{2}$,即AH=$\sqrt{2}$NH,同理可得:NH=HG=$\sqrt{2}$GD,
∴AH=$\sqrt{2}$NH=2HD,又AD=AH+HD=6,
∴HD=$\frac{6}{3}$=2,
∴HG2=22+22,即HG=2$\sqrt{2}$;
∴S1的面积为HG2=8;
∵∠MAO=∠MOA=45°,
∴AM=MO,
∵MO=MN,
∴AM=MB,
∴M为AB的中点,
∴S2的边长为3,
∴S2的面积为3×3=9,
∴S1<S2.
故选B.
点评 本题考查了正方形的性质和等腰直角三角形的性质,熟练掌握等腰直角三角形的性质是解题的关键.

练习册系列答案
相关题目
9.下列各组图形中,属于全等图形的是( )
| A. |  | B. |  | C. |  | D. |  |
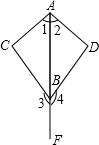 如图,∠3、∠4分别为△ABC与△ABD的外角.已知∠1=∠2,∠3=∠4.求证:AC=AD.
如图,∠3、∠4分别为△ABC与△ABD的外角.已知∠1=∠2,∠3=∠4.求证:AC=AD.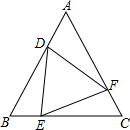 如图,△ABC为等边三角形,边长为1,D,E,F分别为AB,BC,AC上的动点,且AD=BE=CF.若AD=x,△DEF的面积为y.
如图,△ABC为等边三角形,边长为1,D,E,F分别为AB,BC,AC上的动点,且AD=BE=CF.若AD=x,△DEF的面积为y.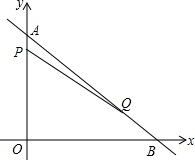 如图,在平面直角坐标系中,点A、点B分别在y轴、x轴的正半轴上,且满足$\sqrt{OA-30}$+(OB-40)2=0,若点P从A点出发,以每秒2个单位长度的速度沿线段AO运动,同时点Q从B点出发,以每秒5个单位长度的速度沿线段BA运动,连接PQ,点P,Q的运动时间为t秒.
如图,在平面直角坐标系中,点A、点B分别在y轴、x轴的正半轴上,且满足$\sqrt{OA-30}$+(OB-40)2=0,若点P从A点出发,以每秒2个单位长度的速度沿线段AO运动,同时点Q从B点出发,以每秒5个单位长度的速度沿线段BA运动,连接PQ,点P,Q的运动时间为t秒.