题目内容
7.已知抛物线y=x2+mx+m-5.(1)求证:不论m为何实数,抛物线与x轴总有两个不同的交点;
(2)当m为何值时,抛物线与x轴的两个交点都在原点左侧?
分析 (1)先列出△与m的函数关系式,然后利用配方法证明△>0即可;
(2)根据两根之和<0,两根之积>0列出不等式求解即可.
解答 解:(1)△=m2-4(m-5)=m2-4m+20=(m-2)2+16>0,
故抛物线与x轴总有两个不同的交点.
(2)由根与系数的关系可知:x1+x2=-m,x1x2=m-5.
∵抛物线与x轴的两个交点都在原点左侧,
∴-m<0,m-5>0.
解得;m>0,m>5.
∴当m>5时,抛物线与x轴的两个交点都在原点左侧.
点评 本题主要考查的是二次函数与x轴的交点问题,将函数问题转化为方程问题是解题的关键.

练习册系列答案
相关题目
19.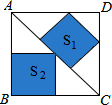 如图,边长为6的大正方形中有两个小正方形,若两个小正方形的面积分别为S1和S2,比较S1与S2的大小( )
如图,边长为6的大正方形中有两个小正方形,若两个小正方形的面积分别为S1和S2,比较S1与S2的大小( )
 如图,边长为6的大正方形中有两个小正方形,若两个小正方形的面积分别为S1和S2,比较S1与S2的大小( )
如图,边长为6的大正方形中有两个小正方形,若两个小正方形的面积分别为S1和S2,比较S1与S2的大小( )| A. | S1>S2 | B. | S1<S2 | C. | S1=S2 | D. | 不能确定 |
17.有个花园占地面积约为 800000平方米,若按比例尺1:2000缩小后,其面积大约相当于( )
| A. | 一个篮球场的面积 | B. | 一张乒乓球台台面的面积 | ||
| C. | 《钱江晚报》一个版面的面积 | D. | 《数学》课本封面的面积 |
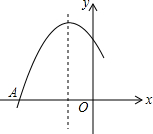 如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),该抛物线的对称轴为直线x=-1,若点C(-$\frac{5}{2}$,y1),D(-$\frac{1}{2}$,y2),E($\frac{3}{2}$,y3)均为函数图象上的点,则y1,y2,y3的大小关系为y3<y1<y2.
如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),该抛物线的对称轴为直线x=-1,若点C(-$\frac{5}{2}$,y1),D(-$\frac{1}{2}$,y2),E($\frac{3}{2}$,y3)均为函数图象上的点,则y1,y2,y3的大小关系为y3<y1<y2.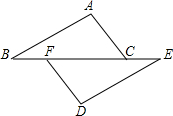 如图,点B、F、C、E在同一条直线上,点A、D在直线BE的两侧,AB∥DE,BF=CE,AB=DE,
如图,点B、F、C、E在同一条直线上,点A、D在直线BE的两侧,AB∥DE,BF=CE,AB=DE,