题目内容
4.已知Rt△OAB的两条直角边在坐标轴上,点A,点B的坐标分别为(0,2),(3,0).(1)写出以点O,A,B为其中三个顶点的平行四边形的第四个顶点C的坐标;
(2)直线l的解析式为y=-2x+2,设点M为直线l上一点,过点M作AB的平行线,交y轴于点N,是否存在这样的点M,使得以M,N,A,B为顶点的四边形是平行四边形?若存在,请求出符合条件的点M的坐标;若不存在,请说明理由.
分析 (1)先由点的坐标求出线段OA,OB的长度,再分情况进行求解,即可解得C点的坐标为(-3,2)或(3,2)或(3,-2);
(2)根据平行四边形的性质先求得M的横坐标,代入直线的解析式即可求得纵坐标.
解答  解:(1)设C点的坐标为(x,y),如图1,
解:(1)设C点的坐标为(x,y),如图1,
∵以点O,A,B,C顶点的四边形是平行四边形,
①当BC=AO时,
∵O(0,0),B(3,0),A(0,2)
∴AO=2,
∴BC=2,
∴C点坐标为C2(3,2)或C3(3,-2)
②BO=AC时,
∵BO=3,
∴AC=3,
∴C点坐标为C1(-3,2),
综上,第四个顶点C的坐标为(-3,2)或(3,2)或(3,-2);
(2)存在,
如图2,过M1作CM1⊥y轴于C,过M1作M1E⊥x轴于E,
∵B的横坐标是3,
∴M1的横坐标是-3,代入直线y=-2x+2得:
y=-2×(-3)+2=8,
∴M1(-3,8),
过M2作DM2⊥y轴于D,
∵B的横坐标是3,
∴M2的横坐标是3,代入直线y=-2x+2得:
y=-2×3+2=-4,
∴M2(3,-4),
∴M点的坐标是:(-3,8)和(3,-4).
点评 本题是一次函数的综合题,考查了平行四边形的判定和性质,一次函数图象上点的坐标特征,分类讨论思想的运用是解题的关键.

练习册系列答案
相关题目
14.下列运算正确的是( )
| A. | (a-b)2=a2-b2 | B. | (a+b)2=a2+ab+b2 | C. | (1+a)(a-1)=a2-1 | D. | (a+b)(b-a)=a2-b2 |
 如图,已知AC=6cm,BC=9cm,∠B=30°,∠D=115°,△ABC∽△DAC,
如图,已知AC=6cm,BC=9cm,∠B=30°,∠D=115°,△ABC∽△DAC,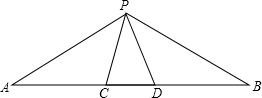 如图,点C,D在线段AB上,P是直线AB外一点,连接PA,PB,PC,PD.已知△PCD是等边三角形,如果CD2=AC•DB,求∠APB的度数.
如图,点C,D在线段AB上,P是直线AB外一点,连接PA,PB,PC,PD.已知△PCD是等边三角形,如果CD2=AC•DB,求∠APB的度数.