题目内容
7.一件工艺品的进价为100元,标价135元出售,每天可售出100件,根据销售统计,一件工艺品每降价1元,则每天可多售出4件,要使每天获得的利润最大,则每件需降价( )| A. | 3.6 元 | B. | 5 元 | C. | 10 元 | D. | 12 元 |
分析 设每件降价x元,每天获得的利润记为W,依据:每天获得的总利润=每件工艺品的利润×每天的销售量,列出函数关系式,配方成顶点式即可得其最值情况.
解答 解:设每件降价x元,每天获得的利润记为W,
根据题意,W=(135-x-100)(100+4x)
=-4x2+40x+3500
=-4(x-5)2+3600,
∵-4<0,
∴当x=5时,W取得最大值,最大值为3600,
即每件降价5元时,每天获得的利润最大,最大利润为3600元.
故选:B.
点评 本题考查了二次函数的应用,主要利用了二次函数的最值问题,表示出降价后的每一件工艺品的利润和销售数量是解题的关键.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目
16.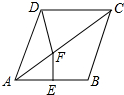 如图,菱形ABCD中,∠BAD=76°,AB的垂直平分线EF交AC于点F,则∠CFD的度数为( )
如图,菱形ABCD中,∠BAD=76°,AB的垂直平分线EF交AC于点F,则∠CFD的度数为( )
 如图,菱形ABCD中,∠BAD=76°,AB的垂直平分线EF交AC于点F,则∠CFD的度数为( )
如图,菱形ABCD中,∠BAD=76°,AB的垂直平分线EF交AC于点F,则∠CFD的度数为( )| A. | 86° | B. | 76° | C. | 66° | D. | 52° |
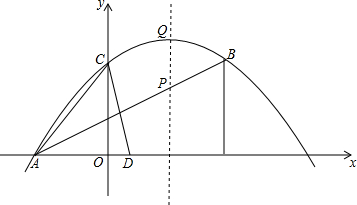 如图,抛物线y=ax2+bx+4的图象经过A(-3,0),B(5,4),与y轴交于点C.
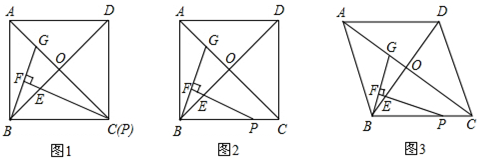
如图,抛物线y=ax2+bx+4的图象经过A(-3,0),B(5,4),与y轴交于点C.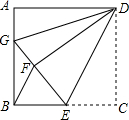 如图,正方形ABCD中,AB=12,点E在边BC上,BE=EC,将△DCE沿DE对折至△DFE,延长EF交边AB于点G,连接DG,BF.
如图,正方形ABCD中,AB=12,点E在边BC上,BE=EC,将△DCE沿DE对折至△DFE,延长EF交边AB于点G,连接DG,BF. 如图,AB为东西走向的一条公路,C是公路旁边的一个村子,现在准备从村庄C修一条公路CD到公路AB,在A点时测得村庄C在它的北偏东45°方向上,沿正东方向4千米后到达B处,此时村庄C在它的北偏西55°方向上,求公路CD的最短长度.(结果精确到0.1千米,参考数据:sin55°≈0.8192,cos55°≈0.5736,tan55°≈1.4281)
如图,AB为东西走向的一条公路,C是公路旁边的一个村子,现在准备从村庄C修一条公路CD到公路AB,在A点时测得村庄C在它的北偏东45°方向上,沿正东方向4千米后到达B处,此时村庄C在它的北偏西55°方向上,求公路CD的最短长度.(结果精确到0.1千米,参考数据:sin55°≈0.8192,cos55°≈0.5736,tan55°≈1.4281)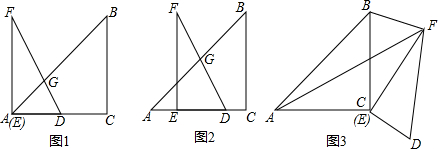
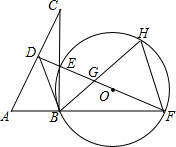 如图,在Rt△ABC中,∠ABC=90°,AC的垂直平分线分别与AC,BC及AB的延长线相交于点D,E,F,⊙O是△BEF的外接圆,∠EBF的平分线交EF于点G,交⊙O于点H,连接BD、FH.
如图,在Rt△ABC中,∠ABC=90°,AC的垂直平分线分别与AC,BC及AB的延长线相交于点D,E,F,⊙O是△BEF的外接圆,∠EBF的平分线交EF于点G,交⊙O于点H,连接BD、FH.