题目内容
13．
如图所示，将长方形纸条的一角沿虚线CD折叠，DE平分∠BDF，则∠CDE=90°．
分析 根据折叠的意义得：∠BDC=∠B′DC，∠BDE=∠FDE；由∠BDC+∠B′DC+∠BDE+∠FDE=180°，得出∠BDE+∠CDB=90°，即可求得∠CDE的值．
解答 解：如图，点B原来的位置为B′，
根据题意得：∠BDC=∠B′DC，∠BDE=∠FDE，
∵∠BDC+∠B′DC+∠BDE+∠FDE=180°，
∴∠CDE=∠BDE+∠CDB=90°．
故答案为90°．
点评 本题考查了翻折变换和角的计算；由翻折变换得出相等的角是解题的关键．
练习册系列答案
相关题目
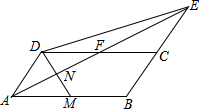如图，在平行四边形ABCD中，AB=6，∠BAD的平分线与BC的延长线交于点E、与DC交于点F，且点F为边DC的中点，∠ADC的平分线交AB于点M，交AE于点N，连接DE
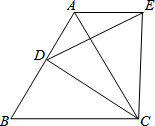如图，点D是等边△ABC的边AB上的一动点，以CD为一边向上作等边△EDC，连接AE，请探究在点D的运动过程中，∠DAE的度数是否会发生变化？如果发生变化，请说明理由；如果不发生变化，请求出这个度数．
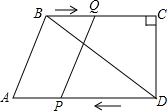如图，在四边形ABCD中，AD∥BC，∠DCB=90°，BC=16，DC=12，AD=21．动点P从点D出发，沿射线DA的方向以每秒2个单位长度的速度运动，同时动点Q从点B出发，在线段BC上以每秒1个单位长度的速度向点C运动，当点P运动到与点A重合时，点Q随之停止．设运动时间为t（秒）．
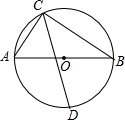如图，AB为⊙O的直径，点C在⊙O上，连接AC和BC，∠ACB的平分线交⊙O于点D，