题目内容
19．（1）解方程组$\left\{\begin{array}{l}{m-\frac{n}{2}=2}\\{2m+3n=12}\end{array}\right.$；（2）已知一次函数y=3x-5与y=2x+b的图象的交点坐标为P（1，-2），试确定方程组$\left\{\begin{array}{l}{y+5=3x}\\{y-2x=b}\end{array}\right.$的解和b的值．
分析 （1）将第一个方程分母化为整数后与第二个相减即可利用加减消元的方法求得方程组的解；
（2）直接根据一次函数和二元一次方程组的关系求解．
解答 解：（1）$\left\{\begin{array}{l}{m-\frac{n}{2}=2①}\\{2m+3n=12②}\end{array}\right.$，
②-①×2得：4n=8，
解得：n=2，
把n=2代入①得：m=3，
所以方程组的解为$\left\{\begin{array}{l}{m=3}\\{n=2}\end{array}\right.$；
（2）∵一次函与y=3x-5与y=2x+b的图象的交点的坐标为P（1，-2）
∴方程组$\left\{\begin{array}{l}{y+5=3x}\\{y-2x=b}\end{array}\right.$的解是$\left\{\begin{array}{l}{x=1}\\{y=-2}\end{array}\right.$，
将点P（1，-2）的坐标代y=2x+b，得b=-4．
点评 本题考查了一次函数和二元一次方程（组）的关系：要准确的将一次函数问题的条件转化为二元一次方程（组），注意自变量取值范围要符合实际意义．
练习册系列答案
课课练江苏系列答案
名牌中学课时作业系列答案
相关题目
20．数轴上A、B两点表示的数分别为-1和$\sqrt{2}$，数轴上点C在点A的左侧，到A点的距离等于点B到点A的距离，则点C所表示的数为（ ）
| A． | $-2+\sqrt{2}$ | B． | $-1+\sqrt{2}$ | C． | $3-\sqrt{2}$ | D． | $-2-\sqrt{2}$ |
现有一块长40cm，宽20cm的长方形铁皮，在它的四个角分别剪去一个大小完全相同的小正方形，用剩余的部分做成一个底面积为300cm2的无盖长方体盒子，请求出剪去的小正方形的边长．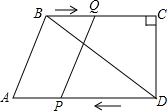
如图，在四边形ABCD中，AD∥BC，∠DCB=90°，BC=16，DC=12，AD=21．动点P从点D出发，沿射线DA的方向以每秒2个单位长度的速度运动，同时动点Q从点B出发，在线段BC上以每秒1个单位长度的速度向点C运动，当点P运动到与点A重合时，点Q随之停止．设运动时间为t（秒）．
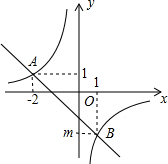如图，一次函数y1=kx+b的图象与反比例函数y2=$\frac{m}{x}$的图象交于A、B两点．