题目内容
若实数x、y、z满足x=4-y，z2=xy-4，求证：x=y．
考点：配方法的应用,非负数的性质：偶次方
专题：证明题
分析：把x=4-y代入z2=xy-4，化简后得到z2=-（y-2）2≥0，所以可得y=2，x=2．
解答：解：∵x=4-y
∴z2=xy-4=（4-y）y-4=-y2+4y-4=-（y-2）2≥0，
所以y=2，x=2．
∴z2=xy-4=（4-y）y-4=-y2+4y-4=-（y-2）2≥0，
所以y=2，x=2．
点评：本题主要考查了配方法的应用以及平方的非负性．本题的关键是得到z2=-（y-2）2．
练习册系列答案
相关题目
某数学兴趣小组在探索“圆的有关相交弦问题”时，
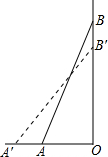如图，梯子AB靠在墙上，梯子的底端A到墙根O的距离为3m，梯子的顶端A向外移动到A′，使梯子的底端A′到墙根O的距离等于4m，同时梯子的顶端B下降至B′，求BB′的长（梯子AB的长为5m）．
如图：在平面直角坐标系中，网格中每一个小正方形的边长为1个单位长度．已知△ABC：
如图，四边形ABCD是梯形，AD∥BC，CA是∠BCD的平分线，且AB⊥AC，若AB=2，AD=3，则tanB的值为