题目内容
1.(1)计算:(2a+1)2-(2a+1)(-1+2a)(2)计算:$\frac{{a}^{2}-1}{a+1}$×$\frac{{a}^{2}-a}{{a}^{2}-2a+1}$-$\frac{ax-a}{x-1}$
(3)解方程:$\frac{x}{x-1}$+$\frac{1}{{x}^{2}-1}$=1.
分析 (1)原式利用完全平方公式及平方差公式化简,去括号合并即可得到结果;
(2)原式两项约分后,合并即可得到结果;
(3)分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解答 解:(1)原式=4a2+4a+1-4a2+1=4a+2;
(2)原式=$\frac{(a+1)(a-1)}{a+1}$•$\frac{a(a-1)}{(a-1)^{2}}$-$\frac{a(x-1)}{x-1}$=a-a=0;
(3)方程两边都乘以(x+1)(x-1)得x(x+1)+1=x2-1,
整理得:x+1=-1,
解得:x=-2,
经检验x=-2是原方程的解.
点评 此题考查了分式的混合运算,整式的混合运算,以及解分式方程,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
12.下列等式中正确的是( )
| A. | -(a-b)=b-a | B. | -(a+b)=-a+b | C. | 2(a+1)=2a+1 | D. | -(3-x)=3+x |
13. 如图,直线EO⊥CD,垂足为O,AB平分∠EOD.则∠EOB等于( )
如图,直线EO⊥CD,垂足为O,AB平分∠EOD.则∠EOB等于( )
 如图,直线EO⊥CD,垂足为O,AB平分∠EOD.则∠EOB等于( )
如图,直线EO⊥CD,垂足为O,AB平分∠EOD.则∠EOB等于( )| A. | 120° | B. | 135° | C. | 125° | D. | 140° |
 二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①2a+b>0;②abc<0;③b2-4ac>0;④a+b+c<0;⑤4a-2b+c<0,其中正确的个数是3.
二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①2a+b>0;②abc<0;③b2-4ac>0;④a+b+c<0;⑤4a-2b+c<0,其中正确的个数是3.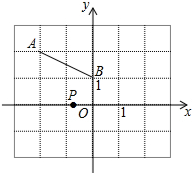 如图,直角坐标系中,点A(-2,2)、B(0,1),点P在x轴上,且△PAB是等腰三角形,则满足条件的点P共4 个.
如图,直角坐标系中,点A(-2,2)、B(0,1),点P在x轴上,且△PAB是等腰三角形,则满足条件的点P共4 个. 如图,河上有一座抛物线桥洞,已知桥下的水面离桥拱顶部3m时,水面宽AB为6m,当水位上升0.5m时:
如图,河上有一座抛物线桥洞,已知桥下的水面离桥拱顶部3m时,水面宽AB为6m,当水位上升0.5m时: