题目内容
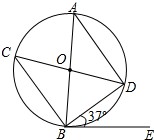 如图,在⊙O中,AB,CD是直径,BE是切线,B为切点,连接AD,BC,BD.
如图,在⊙O中,AB,CD是直径,BE是切线,B为切点,连接AD,BC,BD.(1)求证:△ABD≌△CDB;
(2)若∠DBE=37°,求∠ADC的度数.
考点:切线的性质,全等三角形的判定与性质
专题:证明题
分析:(1)根据AB,CD是直径,可得出∠ADB=∠CBD=90°,再根据HL定理得出Rt△ABD≌Rt△CDB;
(2)由BE是切线,得AB⊥BE,根据∠DBE=37°,得∠BAD,由OA=OD,得出∠ADC的度数.
(2)由BE是切线,得AB⊥BE,根据∠DBE=37°,得∠BAD,由OA=OD,得出∠ADC的度数.
解答:(1)证明:∵AB,CD是直径,
∴∠ADB=∠CBD=90°,
在Rt△ABD和Rt△CDB中,
,
∴Rt△ABD和Rt△CDB(HL);
(2)解:∵BE是切线,
∴AB⊥BE,
∴∠ABE=90°,
∵∠DBE=37°,
∴∠ABD=53°,
∵OA=OD,
∴∠BAD=∠ODA=90°-53°=37°,
∴∠ADC的度数为37°.
∴∠ADB=∠CBD=90°,
在Rt△ABD和Rt△CDB中,
|
∴Rt△ABD和Rt△CDB(HL);
(2)解:∵BE是切线,
∴AB⊥BE,
∴∠ABE=90°,
∵∠DBE=37°,
∴∠ABD=53°,
∵OA=OD,
∴∠BAD=∠ODA=90°-53°=37°,
∴∠ADC的度数为37°.
点评:本题考查了切线的性质以及全等三角形的判定和性质,是基础题,难度不大.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
若a为实数,则
-a
的化简结果正确的是( )
| -a3 |
-
|
A、(-a+1)
| ||
B、(a+1)
| ||
C、(a-1)
| ||
| D、0 |
 已知二次函数y=-x2+bx+c的对称轴为x=2,且经过原点,直线AC解析式为y=kx+4,
已知二次函数y=-x2+bx+c的对称轴为x=2,且经过原点,直线AC解析式为y=kx+4, 在平面直角坐标系中(如图),已知抛物线y=
在平面直角坐标系中(如图),已知抛物线y=
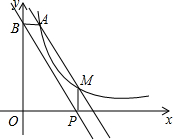 如图,点A(1,6)和点M(m,n)都在反比例函数y=
如图,点A(1,6)和点M(m,n)都在反比例函数y= 如图,△ABC内接于⊙O,∠OAB=20°,则∠C的度数为
如图,△ABC内接于⊙O,∠OAB=20°,则∠C的度数为