题目内容
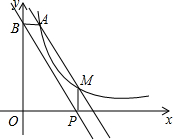 如图,点A(1,6)和点M(m,n)都在反比例函数y=
如图,点A(1,6)和点M(m,n)都在反比例函数y=| k |
| x |
(1)k的值为
(2)当m=3,求直线AM的解析式;
(3)当m>1时,过点M作MP⊥x轴,垂足为P,过点A作AB⊥y轴,垂足为B,试判断直线BP与直线AM的位置关系,并说明理由.
考点:反比例函数综合题
专题:计算题,压轴题,数形结合
分析:(1)将A坐标代入反比例解析式求出k的值即可;
(2)由k的值确定出反比例解析式,将x=3代入反比例解析式求出y的值,确定出M坐标,设直线AM解析式为y=ax+b,将A与M坐标代入求出a与b的值,即可确定出直线AM解析式;
(3)由MP垂直于x轴,AB垂直于y轴,得到M与P横坐标相同,A与B纵坐标相同,表示出B与P坐标,分别求出直线AM与直线BP斜率,由两直线斜率相等,得到两直线平行.
(2)由k的值确定出反比例解析式,将x=3代入反比例解析式求出y的值,确定出M坐标,设直线AM解析式为y=ax+b,将A与M坐标代入求出a与b的值,即可确定出直线AM解析式;
(3)由MP垂直于x轴,AB垂直于y轴,得到M与P横坐标相同,A与B纵坐标相同,表示出B与P坐标,分别求出直线AM与直线BP斜率,由两直线斜率相等,得到两直线平行.
解答:解:(1)将A(1,6)代入反比例解析式得:k=6;
故答案为:6;
(2)将x=3代入反比例解析式y=
得:y=2,即M(3,2),
设直线AM解析式为y=ax+b,
把A与M代入得:
,
解得:a=-2,b=8,
∴直线AM解析式为y=-2x+8;
(3)直线BP与直线AM的位置关系为平行,理由为:
当m>1时,过点M作MP⊥x轴,垂足为P,过点A作AB⊥y轴,垂足为B,
∵A(1,6),M(m,n),且mn=6,即n=
,
∴B(0,6),P(m,0),
∴k直线AM=
=
=
=-
=-
,
k直线BP=
=-
,
即k直线AM=k直线BP,
则BP∥AM.
故答案为:6;
(2)将x=3代入反比例解析式y=
| 6 |
| x |
设直线AM解析式为y=ax+b,
把A与M代入得:
|
解得:a=-2,b=8,
∴直线AM解析式为y=-2x+8;
(3)直线BP与直线AM的位置关系为平行,理由为:

当m>1时,过点M作MP⊥x轴,垂足为P,过点A作AB⊥y轴,垂足为B,
∵A(1,6),M(m,n),且mn=6,即n=
| 6 |
| m |
∴B(0,6),P(m,0),
∴k直线AM=
| 6-n |
| 1-m |
6-
| ||
| 1-m |
| 6m-6 |
| -m(m-1) |
| 6(m-1) |
| m(m-1) |
| 6 |
| m |
k直线BP=
| 6-0 |
| 0-m |
| 6 |
| m |
即k直线AM=k直线BP,
则BP∥AM.
点评:此题属于反比例函数综合题,涉及的知识有:待定系数法确定函数解析式,以及两直线平行与斜率之间的关系,熟练掌握待定系数法是解本题第二问的关键.

练习册系列答案
相关题目
北京到马来西亚首都吉隆坡的距离约为46 500 000m.用科学记数法表示46 500 000,应记为( )
| A、46.5×106 |
| B、4.65×106 |
| C、4.65×107 |
| D、0.465×108 |
 在平面直角坐标系xOy中,抛物线y=2x2+mx+n经过点A(0,-2),B(3,4).
在平面直角坐标系xOy中,抛物线y=2x2+mx+n经过点A(0,-2),B(3,4).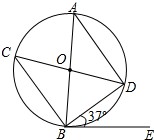 如图,在⊙O中,AB,CD是直径,BE是切线,B为切点,连接AD,BC,BD.
如图,在⊙O中,AB,CD是直径,BE是切线,B为切点,连接AD,BC,BD.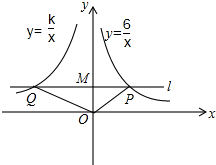 如图,在平面直角坐标系中,过点M(0,2)的直线l与x轴平行,且直线l分别与反比例函数y=
如图,在平面直角坐标系中,过点M(0,2)的直线l与x轴平行,且直线l分别与反比例函数y=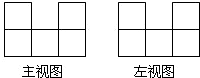 在桌上摆着一个由若干个相同正方体组成的几何体,其主视图和左视图如图所示,设组成这个几何体的小正方体的个数为n,则n的最小值为
在桌上摆着一个由若干个相同正方体组成的几何体,其主视图和左视图如图所示,设组成这个几何体的小正方体的个数为n,则n的最小值为 如图,直线MN与⊙O相切于点M,ME=EF且EF∥MN,则cos∠E=
如图,直线MN与⊙O相切于点M,ME=EF且EF∥MN,则cos∠E=