题目内容

8．解方程
（1）x2+4x+2=0
（2）（x-2）2+2=x．

分析 （1）根据配方法可以解答此方程；
（2）根据提公因式法可以解答此方程．

解答 解：（1）x2+4x+2=0
x2+4x=-2
x2+4x+4=-2+4
（x+2）2=2，
∴x+2=±$\sqrt{2}$，
∴${x}_{1}=-2+\sqrt{2}$，${x}_{2}=-2-\sqrt{2}$；
（2）（x-2）2+2=x
（x-2）2+（2-x）=0
（x-2）[（x-2）-1]=0
（x-2）（x-3）=0，
∴x-2=0或x-3=0，
解得，x1=2，x2=3．

点评 本题考查解一元二次方程--因式分解法（配方法），解题的关键是根据方程选取合适的方法进行解答．

练习册系列答案
相关题目
7．慧慧和龙龙在数学活动课上，对方程$\frac{2}{3x-3}$+$\frac{3}{2x-2}$=$\frac{13}{3}$的解法进行了讨论．请阅读下面的对话．

现在，请你根据对话的内容解分式方程$\frac{9}{x+3}$-$\frac{15}{3x+9}$=1．
8．画出函数y=-2x+3的图象，结合图象求：
（1）方程-2x+3=0的解；
（2）不等式-2x+3＜0的解集；
（3）不等式组-3≤-2x+3≤7的解集．
5．已知关于x的方程x2-2x+k=0．
（1）方程有实数根，求k的取值范围；
（2）若方程的一个根是-1，求另一个根及k的值．
3．（1）|-3|+（$\root{3}{27}$-1）0-$\sqrt{16}$+（$\frac{1}{3}$）-1；
（2）解方程组$\left\{\begin{array}{l}{3（x-y-1）=9-y}\\{\frac{x}{2}+\frac{y}{3}=2}\end{array}\right.$；
（3）求x的值：25（x+2）2-36=0．
13．列方程解应用题
某商店用2000元购进一批小学生书包，出售后发现供不应求，商店又购进第二批同样的书包，所购数量是第一批购进数量的3倍，但单价贵了2元，结果购买第二批书包用了6600元．
（1）请求出第一批每只书包的进价；
（2）该商店第一批和第二批分别购进了多少只书包；
（3）若商店销售这两批书包时，每个售价都是30元，全部售出后，商店共盈利多少元？
20．巴蜀中学对本校初2017届500名学生中中考参加体育加试测试情况进行调查，根据男生1000米及女生800米测试成绩整理，绘制成不完整的统计图，（图①，图②），请根据统计图提供的信息，回答下列问题：
（1）该校毕业生中男生有300人；扇形统计图中a=12；
（2）补全条形统计图；
（3）若500名学生中随机抽取一名学生，这名学生该项成绩在8分及8分以下的概率是多少？
17．已知x=2是一元二次方程2x2+x-m=0的一个解，则m的值是（　　）
A．-8B．10C．-4D．8
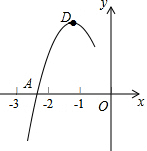18．抛物线y=ax2+bx+c的顶点为D（-1，2），与x轴的一个交点A在点（-3，0）和（-2，0）之间，其部分图象如图所示，则下列结论：①b2-4ac＜0；②a+b+c＜0；③2a+b=0；④c-a=2；⑤4ac-8a=b2；⑥方程ax2+bx+c-1=0有两个相等的实数根．其中正确结论的个数为（　　）
A．3个B．4个C．5个D．6个

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网