题目内容
 如图,已知扇形OAB的圆心角为135°,半径为1,则弓形AMB的面积为多少?
如图,已知扇形OAB的圆心角为135°,半径为1,则弓形AMB的面积为多少?考点:扇形面积的计算
专题:
分析:过点A作AD⊥BO的延长线于点D,先根据∠AOB=135°求出∠AOD的度数,由锐角三角函数的定义得出AD的长,再根据S弓形AMB=S扇形AOB-S△AOB即可得出结论.
解答: 解:过点A作AD⊥BO的延长线于点D,
解:过点A作AD⊥BO的延长线于点D,
∵∠AOB=135°,
∴∠AOD=180°-135°=45°.
∵OA=1,
∴AD=OA•sin45°=
,
∴S弓形AMB=S扇形AOB-S△AOB=
-
×1×
=
-
.
答:弓形AMB的面积为
-
.
 解:过点A作AD⊥BO的延长线于点D,
解:过点A作AD⊥BO的延长线于点D,∵∠AOB=135°,
∴∠AOD=180°-135°=45°.
∵OA=1,
∴AD=OA•sin45°=
| ||
| 2 |
∴S弓形AMB=S扇形AOB-S△AOB=
| 135π×12 |
| 360 |
| 1 |
| 2 |
| ||
| 2 |
| 3π |
| 8 |
| ||
| 4 |
答:弓形AMB的面积为
| 3π |
| 8 |
| ||
| 4 |
点评:本题考查的是扇形面积的计算,熟记扇形的面积公式是解答此题的关键.

练习册系列答案
相关题目
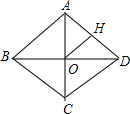 如图,菱形ABCD中,对角线AC、BD相交于点O,H为AD边中点,菱形ABCD的周长为32,则OH的长等于( )
如图,菱形ABCD中,对角线AC、BD相交于点O,H为AD边中点,菱形ABCD的周长为32,则OH的长等于( )| A、4 | B、8 | C、16 | D、18 |
 如图,若图中所有的三角形都是直角三角形,且∠A=α,AE=1,求AB的长.
如图,若图中所有的三角形都是直角三角形,且∠A=α,AE=1,求AB的长. 已知△ABC(如图)
已知△ABC(如图) 如图,圆内接四边形ABCD中,∠A=62°,则∠C=
如图,圆内接四边形ABCD中,∠A=62°,则∠C=