题目内容
已知,等腰直角三角形ABC,∠C=90°,CA=CB,直线MN⊥直线PQ,垂足为O,

进行如下操作,探究:
(1)将直角三角形ABC按①中方式放置,D是射线OM上一点,连结BD,过A点作AH⊥BD于点H,交OB于点E,
求证:OE=OD;

(2)将直角三角形ABC按②中方式放置,点A在OM上,点C在OP上,BC交MN于点F,过点B作BG⊥MN,若AF恰好平分∠CAB,猜想BG与AF之间有怎样的数量关系,并证明;
(3)将直角三角形ABC按③中方式放置,若OA=5,点C在射线OP上运动,作IC⊥OC且IC=OC,连结BI,交PQ于K,当点C运动时,KC的长是否发生改变?若变化求出KC长度的范围,若不变求KC的长.

进行如下操作,探究:
(1)将直角三角形ABC按①中方式放置,D是射线OM上一点,连结BD,过A点作AH⊥BD于点H,交OB于点E,
求证:OE=OD;

(2)将直角三角形ABC按②中方式放置,点A在OM上,点C在OP上,BC交MN于点F,过点B作BG⊥MN,若AF恰好平分∠CAB,猜想BG与AF之间有怎样的数量关系,并证明;
(3)将直角三角形ABC按③中方式放置,若OA=5,点C在射线OP上运动,作IC⊥OC且IC=OC,连结BI,交PQ于K,当点C运动时,KC的长是否发生改变?若变化求出KC长度的范围,若不变求KC的长.
考点:全等三角形的判定与性质
专题:
分析:(1)运用AAS公理,证明△AOE≌△BOD,即可解决问题.
(2)如图,作辅助线;类比(1)中的方法证明AF=BR;然后证明BG=RG,即可解决问题.
(3)如图,作辅助线;首先证明BR=OC,进而得到IC=BR;证明RK=KC,即可解决问题.
(2)如图,作辅助线;类比(1)中的方法证明AF=BR;然后证明BG=RG,即可解决问题.
(3)如图,作辅助线;首先证明BR=OC,进而得到IC=BR;证明RK=KC,即可解决问题.
解答: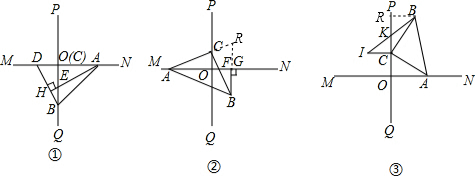 (1)证明:如图①,
(1)证明:如图①,
∵AH⊥BD,AO⊥OE
∴∠ODB+∠DAH
=∠OEA+∠DAH,
∴∠ODB=∠OEA,
在△AOE与△BOD中,
,
∴△AOE≌△BOD(AAS),
∴OE=OD.
(2)如图②,分别延长AC、BG,交于点R;
类比(1)中的方法,同理可证△AGF≌△BGR,
∴AF=BR;
在△AGR与△AGB中,
,
∴△AGR≌△AGB(ASA),
∴BG=GR,
∴AF=BR=2BG.
(3)KC的长度不变;理由如下:如图③,过点B作BR⊥CP于点R;
∵∠BRC=∠ACB=∠AOC=90°,
∴∠RBC+∠BCR=∠BCR+∠ACO,
∴∠RBC=∠ACO;
在△RBC与△OCA中,
,
∴△RBC≌△OCA(AAS),
∴BR=OC,RC=OA;而IC=OC,
∴BR=IC;而BR∥IC,
∴△BRK∽△ICK,
∴
=
=1,
∴RK=KC,KC=
RC=
OA为定值,不变.
 (1)证明:如图①,
(1)证明:如图①,∵AH⊥BD,AO⊥OE
∴∠ODB+∠DAH
=∠OEA+∠DAH,
∴∠ODB=∠OEA,
在△AOE与△BOD中,
|
∴△AOE≌△BOD(AAS),
∴OE=OD.
(2)如图②,分别延长AC、BG,交于点R;
类比(1)中的方法,同理可证△AGF≌△BGR,
∴AF=BR;
在△AGR与△AGB中,
|
∴△AGR≌△AGB(ASA),
∴BG=GR,
∴AF=BR=2BG.
(3)KC的长度不变;理由如下:如图③,过点B作BR⊥CP于点R;
∵∠BRC=∠ACB=∠AOC=90°,
∴∠RBC+∠BCR=∠BCR+∠ACO,
∴∠RBC=∠ACO;
在△RBC与△OCA中,
|
∴△RBC≌△OCA(AAS),
∴BR=OC,RC=OA;而IC=OC,
∴BR=IC;而BR∥IC,
∴△BRK∽△ICK,
∴
| BR |
| IC |
| RK |
| KC |
∴RK=KC,KC=
| 1 |
| 2 |
| 1 |
| 2 |
点评:该题主要考查了全等三角形的判定及其性质的应用问题;解题的关键是作辅助线,灵活运用全等三角形的判定及其性质等来分析、判断、推理或解答.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
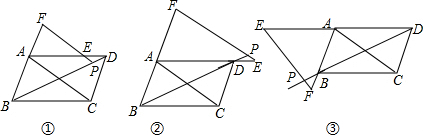
 如图,点O是?ABCD对角线AC中点,EF经过点O交AD于点E,交BC于点F,连接BE,DF
如图,点O是?ABCD对角线AC中点,EF经过点O交AD于点E,交BC于点F,连接BE,DF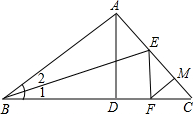 如图,已知∠BAC=90°,AD⊥BC,∠1=∠2,EF⊥BC,FM⊥AC,说明FM=FD的理由.
如图,已知∠BAC=90°,AD⊥BC,∠1=∠2,EF⊥BC,FM⊥AC,说明FM=FD的理由. 已知△ABC,AB=AC=5cm,BC=8cm,P为AC上一动点,沿着折线CAB运动(当到达B时停止),Q为CB上一动点,沿CB运动(到B时停止),若P,Q分别同时从C点出发,以2cm/s和1cm/s的速度沿折线CAB和CB运动,问,何时PQ截△ABC两边所形成的三角形与原三角形相似?是位似图形吗?
已知△ABC,AB=AC=5cm,BC=8cm,P为AC上一动点,沿着折线CAB运动(当到达B时停止),Q为CB上一动点,沿CB运动(到B时停止),若P,Q分别同时从C点出发,以2cm/s和1cm/s的速度沿折线CAB和CB运动,问,何时PQ截△ABC两边所形成的三角形与原三角形相似?是位似图形吗? 如图是一个多边形,求∠A1+∠A2+∠A3+…+∠A23+∠A24的度数.
如图是一个多边形,求∠A1+∠A2+∠A3+…+∠A23+∠A24的度数. 有一块形状为平行四边形的铁片,用AB表示较长的一边,AD、BC表示较短的边,现有AB=2AD.现在想用这块铁片截一个直角三角形,并且希望以AB为斜边,直角顶点在CD上,问此想法是否可行?如果可行的话,请说明应该怎样截;如果不行,请说明理由.
有一块形状为平行四边形的铁片,用AB表示较长的一边,AD、BC表示较短的边,现有AB=2AD.现在想用这块铁片截一个直角三角形,并且希望以AB为斜边,直角顶点在CD上,问此想法是否可行?如果可行的话,请说明应该怎样截;如果不行,请说明理由. 如图,已知A(-4,0.5),B(-1,2)是一次函数y=ax+b与反比例函数
如图,已知A(-4,0.5),B(-1,2)是一次函数y=ax+b与反比例函数