Question

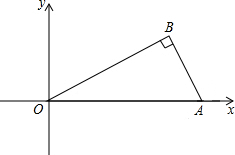已知在Rt△OAB中，∠B=90°，AO=2

3

，BA=2，把△OAB按如图方式放置在直角坐标系中，使O与原点重合，点A落在x轴正半轴上，求点B的坐标．

Answer 1

考点：勾股定理,坐标与图形性质

专题：计算题

分析：过B作BD⊥x轴，交x轴于点D，在直角三角形AOB中，利用勾股定理求出OB的长，由三角形BOD与三角形AOB相似，由相似得比例，求出OD与BD的长，即可确定出B坐标．

解答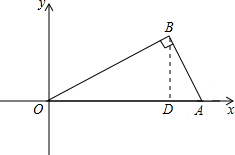：解：过B作BD⊥x轴，交x轴于点D，
在Rt△AOB中，AO=2

3

，BA=2，
根据勾股定理得：OB=

OA2-BA2

=2

2

，
∵∠ODB=∠OBA=90°，∠BOD=∠AOB，
∴△BOD∽△AOB，
∴

OB

OA

=

BD

BA

=

OD

OB

，即

2 2

2 3

=

BD

2

=

OD

2 2

，
解得：BD=

2 6

3

，OD=

4 3

3

，
则D坐标为（

4 3

3

，

2 6

3

）．

点评：此题考查了勾股定理，以及坐标与图形性质，熟练掌握勾股定理是解本题的关键．