题目内容
 如图,在一笔直的海岸线l上有A、B两个观测站,A在B的正东方向,BP=3
如图,在一笔直的海岸线l上有A、B两个观测站,A在B的正东方向,BP=3| 3 |
(1)求A、B两个观测站之间的距离;
(2)小船从点P处沿射线AP的方向以
| 3 |
考点:解直角三角形的应用-方向角问题
专题:
分析:(1)过点P作PD⊥AB于点D,先解Rt△PBD,得到BD和PD的长,再解Rt△PAD,得到AD和AP的长,然后根据BD+AD=AB,即可求解;
(2)过点B作BF⊥AC于点F,先解Rt△ABF,得出BF和AF的长,再解Rt△BCF,得出CF的长,可求PC=AF+CF-AP,从而求解.
(2)过点B作BF⊥AC于点F,先解Rt△ABF,得出BF和AF的长,再解Rt△BCF,得出CF的长,可求PC=AF+CF-AP,从而求解.
解答: 解:(1)如图,过点P作PD⊥AB于点D.
解:(1)如图,过点P作PD⊥AB于点D.
在Rt△PBD中,∠BDP=90°,∠PBD=90°-45°=45°,
∴BD=PD=
km.
在Rt△PAD中,∠ADP=90°,∠PAD=90°-60°=30°,
∴AD=
PD=
km,PA=3
.
∴AB=BD+AD=(
+
)km;
(2)如图,过点B作BF⊥AC于点F.
根据题意得:∠ABC=105°,
在Rt△ABF中,∠AFB=90°,∠BAF=30°,
∴BF=
AB=(
+
)km,AF=
AB=(
+
)km.
在△ABC中,∠C=180°-∠BAC-∠ABC=45°.
在Rt△BCF中,∠BFC=90°,∠C=45°,
∴CF=BF=(
+
)km,
∴PC=AF+CF-AP=
km.
故小船沿途考察的时间为
÷
=
小时.
 解:(1)如图,过点P作PD⊥AB于点D.
解:(1)如图,过点P作PD⊥AB于点D.在Rt△PBD中,∠BDP=90°,∠PBD=90°-45°=45°,
∴BD=PD=
3
| ||
| 2 |
在Rt△PAD中,∠ADP=90°,∠PAD=90°-60°=30°,
∴AD=
| 3 |
9
| ||
| 2 |
| 6 |
∴AB=BD+AD=(
3
| ||
| 2 |
9
| ||
| 2 |
(2)如图,过点B作BF⊥AC于点F.
根据题意得:∠ABC=105°,
在Rt△ABF中,∠AFB=90°,∠BAF=30°,
∴BF=
| 1 |
| 2 |
3
| ||
| 4 |
9
| ||
| 4 |
| ||
| 2 |
9
| ||
| 4 |
9
| ||
| 4 |
在△ABC中,∠C=180°-∠BAC-∠ABC=45°.
在Rt△BCF中,∠BFC=90°,∠C=45°,
∴CF=BF=(
3
| ||
| 4 |
9
| ||
| 4 |
∴PC=AF+CF-AP=
9
| ||
| 2 |
故小船沿途考察的时间为
9
| ||
| 2 |
| 3 |
3
| ||
| 2 |
点评:本题考查了解直角三角形的应用-方向角问题,难度适中.通过作辅助线,构造直角三角形是解题的关键.

练习册系列答案
相关题目
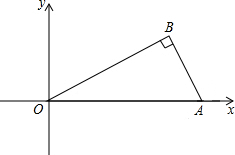 已知在Rt△OAB中,∠B=90°,AO=
已知在Rt△OAB中,∠B=90°,AO= 如图,AD⊥CD,AB=10,BC=20,∠A=∠C=30°.求:
如图,AD⊥CD,AB=10,BC=20,∠A=∠C=30°.求: