题目内容
17. 如图,在?ABCD中,过对角线BD上一点P作EF∥BC,GH∥AB,且CG=2BG,S△BPG=1,则S?AEPH=4.
如图,在?ABCD中,过对角线BD上一点P作EF∥BC,GH∥AB,且CG=2BG,S△BPG=1,则S?AEPH=4.
分析 由条件可证明四边形HPFD、BEPG为平行四边形,可证明S四边形AEPH=S四边形PFCG.,再利用面积的和差可得出四边形AEPH和四边形PFCG的面积相等,由已知条件即可得出答案.
解答 解:∵EF∥BC,GH∥AB,
∴四边形HPFD、BEPG、AEPH、CFPG为平行四边形,
∴S△PEB=S△BGP,
同理可得S△PHD=S△DFP,S△ABD=S△CDB,
∴S△ABD-S△PEB-S△PHD=S△CDB-S△BGP-S△DFP,
即S四边形AEPH=S四边形PFCG.
∵CG=2BG,S△BPG=1,
∴S四边形AEPH=S四边形PFCG=4×1=4;
故答案为:4.
点评 本题主要考查平行四边形的判定和性质,掌握平行四边形的判定和性质是解题的关键,即①两组对边分别平行?四边形为平行四边形,②两组对边分别相等?四边形为平行四边形,③一组对边平行且相等?四边形为平行四边形,④两组对角分别相等?四边形为平行四边形,⑤对角线互相平分?四边形为平行四边形.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.关于反比例函数y=$\frac{3}{x}$,下列说法中正确的是( )
| A. | 它的图象分布在第二、四象限 | B. | 它的图象过点(-6,-2) | ||
| C. | 当x<0时,y的值随x的增大而减小 | D. | 与y轴的交点是(0,3) |
12.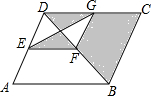 小强喜欢玩飞镖游戏,一天他用平行四边形做了一个飞镖盘,如图所示,?ABCD中,过对角线BD上任一点F分别作FE∥AB,FG∥BC分别交AD,CD于点E,G,连接EG,则小强随机掷一次飞镖,飞镖落在阴影部分的概率是( )
小强喜欢玩飞镖游戏,一天他用平行四边形做了一个飞镖盘,如图所示,?ABCD中,过对角线BD上任一点F分别作FE∥AB,FG∥BC分别交AD,CD于点E,G,连接EG,则小强随机掷一次飞镖,飞镖落在阴影部分的概率是( )
 小强喜欢玩飞镖游戏,一天他用平行四边形做了一个飞镖盘,如图所示,?ABCD中,过对角线BD上任一点F分别作FE∥AB,FG∥BC分别交AD,CD于点E,G,连接EG,则小强随机掷一次飞镖,飞镖落在阴影部分的概率是( )
小强喜欢玩飞镖游戏,一天他用平行四边形做了一个飞镖盘,如图所示,?ABCD中,过对角线BD上任一点F分别作FE∥AB,FG∥BC分别交AD,CD于点E,G,连接EG,则小强随机掷一次飞镖,飞镖落在阴影部分的概率是( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{5}$ |
9.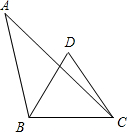 如图,点D为线段AB与线段BC的垂直平分线的交点,连接AC、BD、DC,若∠A=35°,∠ABD=44°,则∠DCA的度数为( )
如图,点D为线段AB与线段BC的垂直平分线的交点,连接AC、BD、DC,若∠A=35°,∠ABD=44°,则∠DCA的度数为( )
 如图,点D为线段AB与线段BC的垂直平分线的交点,连接AC、BD、DC,若∠A=35°,∠ABD=44°,则∠DCA的度数为( )
如图,点D为线段AB与线段BC的垂直平分线的交点,连接AC、BD、DC,若∠A=35°,∠ABD=44°,则∠DCA的度数为( )| A. | 10° | B. | 18° | C. | 15° | D. | 9° |
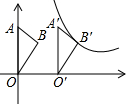 如图,在平面直角坐标系xOy中,点A在y轴上,点B的坐标为(1,2),将△AOB沿x轴向右平移得到△A′O′B′,点B的对应点B′恰好在函数y=$\frac{6}{x}$(x>0)的图象上,此时点A移动的距离为2.
如图,在平面直角坐标系xOy中,点A在y轴上,点B的坐标为(1,2),将△AOB沿x轴向右平移得到△A′O′B′,点B的对应点B′恰好在函数y=$\frac{6}{x}$(x>0)的图象上,此时点A移动的距离为2. 在矩形ABCD中,AB=6,BC=7,E、F、M分别为AB、BC、CD边上的点,连接EF、FM、ME,且AE=3,DM=2,若∠EFM=90°,BF>FC,则BF=( )
在矩形ABCD中,AB=6,BC=7,E、F、M分别为AB、BC、CD边上的点,连接EF、FM、ME,且AE=3,DM=2,若∠EFM=90°,BF>FC,则BF=( )