题目内容
18．将抛物线y=x2+4x+3先向右平移3个单位，再向下平移2个单位，则平移后的抛物线解析式为（ ）| A． | y=（x-1）2-3 | B． | y=x2+x+1 | C． | y=x2+4（x-3）+1 | D． | y=（x+3）2+4（x+3）+1 |
分析 先把抛物线y=x2+4x+3化为顶点式的形式，再根据二次函数变化规律：左加右减，上加下减，即可得出变化后解析式．
解答 解：抛物线y=x2+4x+3可化y=（x+2）2-1，
将抛物线y=x2+4x+3先向右平移3个单位，再向下平移2个单位，
则平移后的抛物线解析式为y=（x+2-3）2-1-2，即y=（x-1）2-3，
故选A．
点评 此题考查了二次函数图象与几何变换，熟记平移规律“左加右减，上加下减”，是解题关键．也考查了配方法．
练习册系列答案
相关题目
3．
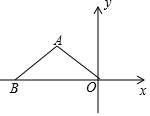如图，已知等腰△ABO的底边BO在x轴上，且BO=8，AB=AO=5，点A的坐标是（ ）
如图，已知等腰△ABO的底边BO在x轴上，且BO=8，AB=AO=5，点A的坐标是（ ）| A． | （-3，4） | B． | （3，-4） | C． | （-4，3） | D． | （4，-3） |
7．在Rt△ABC中，∠C=90°，a=1，b=$\sqrt{3}$，则∠A=（ ）
| A． | 30° | B． | 45° | C． | 60° | D． | 90° |