题目内容
16. 如图,在四边形ABCD中,AB∥CD,且∠BAE=31°,∠CDE=59°,AE=2,DE=4,求AD的长.
如图,在四边形ABCD中,AB∥CD,且∠BAE=31°,∠CDE=59°,AE=2,DE=4,求AD的长.
分析 根据平行线的性质求出∠AED=90°,根据勾股定理计算即可.
解答 解:∵AB∥CD,
∴∠BAD+∠CDA=180°,
∴∠EAD+∠EDA=180°-31°-59°=90°,
∴∠AED=90°,
∴AD=$\sqrt{A{E}^{2}+D{E}^{2}}$=2$\sqrt{5}$.
点评 本题考查的是勾股定理的应用,直角三角形的两条直角边长分别是a,b,斜边长为c,那么a2+b2=c2.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.下列各组数据中,结果相等的是( )
| A. | (-1)4与-14 | B. | -|-3|与-(-3) | C. | -(-1)2015与(-1)2016 | D. | -(-3)与+(-3) |
1.下列命题是真命题的是( )
| A. | 同旁内角互补 | |
| B. | 三角形的一个外角等于它的两个内角之和 | |
| C. | 三角形的一个外角大于内角 | |
| D. | 直角三角形的两锐角互余 |
8.下列运算正确的是( )
| A. | (3x3)2=9x6 | B. | 2x3•x2=2x6 | C. | x3+x2=x5 | D. | x6÷x3=x2 |
 如图AB与CD平行,∠1=45°,∠D=45°,
如图AB与CD平行,∠1=45°,∠D=45°, 如图,直线AB、CD相交于O,∠AOC=28°,OE平分∠AOD,求∠EOC的度数.
如图,直线AB、CD相交于O,∠AOC=28°,OE平分∠AOD,求∠EOC的度数.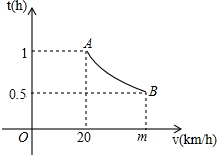 一辆汽车匀速通过某段公路,所需时间t(h)与行驶速度v(km/h)满足函数关系:t=$\frac{k}{v}$,其图象为如图所示的一段曲线且端点为A(20,1)和B(m,0.5).
一辆汽车匀速通过某段公路,所需时间t(h)与行驶速度v(km/h)满足函数关系:t=$\frac{k}{v}$,其图象为如图所示的一段曲线且端点为A(20,1)和B(m,0.5).