题目内容
在一次期中考试中,某校八年级(1)(2)两班学生的数学成绩(成绩均为整十数)统计如下:
请你根据所学的统计知识,分别从平均数、众数、方差等不同角度判断这两个班的考试成绩谁优谁次.
| 成绩(分) | 50 | 60 | 70 | 80 | 90 | 100 | |
| 人数 | (1)班 | 3 | 5 | 16 | 3 | 11 | 12 |
| (2)班 | 2 | 5 | 11 | 12 | 13 | 7 | |
考点:方差,算术平均数,众数
专题:
分析:分别利用平均数以及众数方差求法得出即可.
解答:解:
(1)班=
(50×3+5×60+70×16+80×3+90×11+100×12)=80,
(2)班=
(50×2+5×60+70×11+80×12+90×13+100×7)=80,
(1)班众数为:70,(2)班众数为:90,
=
[(50-80)2+(50-80)2+…+(100-80)2]=284,
=
[(50-80)2+(50-80)2+…+(100-80)2]=180,
∴从平均数看,两个班成绩相同,从众数看,(2)班成绩较好,
从方差看(2)班成绩较稳定.
. |
| x |
| 1 |
| 50 |
. |
| x |
| 1 |
| 50 |
(1)班众数为:70,(2)班众数为:90,
| S | 2 (1)班 |
| 1 |
| 50 |
| S | 2 (2) |
| 1 |
| 50 |
∴从平均数看,两个班成绩相同,从众数看,(2)班成绩较好,
从方差看(2)班成绩较稳定.
点评:本题考查了平均数以及众数和方差计算方法.一般地设n个数据,x1,x2,…xn的平均数为
,
=
(x1+x2+…+xn),则方差S2=
[(x1-
)2+(x2-
)2+…+(xn-
)2].
. |
| x |
. |
| x |
| 1 |
| n |
| 1 |
| n |
. |
| x |
. |
| x |
. |
| x |

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
下列各式计算结果不正确的是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…照如图所示的方式放置,点A1,A2,A3,…和点C1,C2,C3,…分别在直线y=kx+b(k>0)和x轴上,已知点B1(1,1),B2(3,2),则B3的坐标是( )
如图,正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…照如图所示的方式放置,点A1,A2,A3,…和点C1,C2,C3,…分别在直线y=kx+b(k>0)和x轴上,已知点B1(1,1),B2(3,2),则B3的坐标是( )| A、(12,9) |
| B、(10,7) |
| C、(8,5) |
| D、(7,4) |
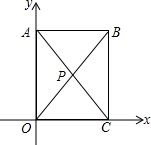 如图,长方形ABCO对角线BO与AC的交点P到相对两边距离相等.若C点(2,0),P(1,2),请写出A,B坐标,你发现A,P,C三点横坐标有什么关系呢?纵坐标呢?
如图,长方形ABCO对角线BO与AC的交点P到相对两边距离相等.若C点(2,0),P(1,2),请写出A,B坐标,你发现A,P,C三点横坐标有什么关系呢?纵坐标呢? 如图,若∠BCD=∠B+∠D,则AB与DE平行,试说明理由.
如图,若∠BCD=∠B+∠D,则AB与DE平行,试说明理由.