题目内容
15.牧场上有三块牧地,第一块12公顷,第二块22公顷,第三块15公顷,第一块地可供96头牛吃7天,第二块地可供220头牛吃5天,那么第三块地可供多少头牛吃35天?(每公顷牧场上原有草量相等,且每公顷牧地上每天生长草量相等)分析 设牧场每公顷有草x千克,每天每公顷新增y千克,每头牛每天吃草a千克,根据第一块地可供96头牛吃7天,第二块地可供220头牛吃5天,列方程求解,然后求出第三块地可供的头数.
解答 解:设牧场每公顷有草x千克,每天每公顷新增y千克,每头牛每天吃草a千克,
由题意得$\left\{\begin{array}{l}{12x+12×7y=96a×7}\\{22x+22×5y=220a×5}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=35a}\\{y=3a}\end{array}\right.$,
则第三块地35天可供的头数为:$\frac{15×35a+35×3a}{35a}$=18(头).
答:第三块地可供18头牛吃35天.
点评 本题考查了二元一次方程组的应用,解答本题的关键是读懂题意,设出未知数,找出合适的等量关系,列方程组求解.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目

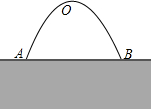 如图,桥拱是抛物线形,当水位线在AB位置时,水面宽为12m.此时水面与轿拱的最高点O距离是9米,当水面与桥拱的最高点O距离不小于4m,该桥可以安全通车,否则就必须要封闭桥面,问当桥拱内的水面宽在什么范围内,该轿可以安全通车?
如图,桥拱是抛物线形,当水位线在AB位置时,水面宽为12m.此时水面与轿拱的最高点O距离是9米,当水面与桥拱的最高点O距离不小于4m,该桥可以安全通车,否则就必须要封闭桥面,问当桥拱内的水面宽在什么范围内,该轿可以安全通车? 如图,在直角坐标系xOy中,直线y=$\frac{1}{2}$x+2与x轴,y轴分别交于A,B两点,以AB为边在第二象限内作矩形ABCD,使AD=$\sqrt{5}$.
如图,在直角坐标系xOy中,直线y=$\frac{1}{2}$x+2与x轴,y轴分别交于A,B两点,以AB为边在第二象限内作矩形ABCD,使AD=$\sqrt{5}$. 如图,直线a∥b∥c,若$\frac{AC}{CE}$=$\frac{2}{3}$,BD=3,则DF的长为4.5.
如图,直线a∥b∥c,若$\frac{AC}{CE}$=$\frac{2}{3}$,BD=3,则DF的长为4.5.