题目内容
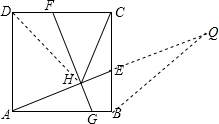
 如图,正方形ABCD中,E、F分别为边BC、DC上的点,且BE=FD,连接AE,过点F作FH⊥AE,交AB于点G,连接CH.
如图,正方形ABCD中,E、F分别为边BC、DC上的点,且BE=FD,连接AE,过点F作FH⊥AE,交AB于点G,连接CH.(1)若DF=2,tan∠EAB=
| 1 |
| 3 |
(2)求证:EH+FH=
| 2 |
考点:正方形的性质,全等三角形的判定与性质
专题:几何图形问题
分析:(1)由条件BE=DF可知BE=2,又因为tan∠EAB=
,所以AB=6,由勾股定理即可求出AE的长;
(2)延长AE到Q,使EQ=FH,连接DQ,证△DFH≌△DEQ,推出DQ=DH,∠QDE=∠FDH,求出∠QDH=∠QDE+∠EDH=∠ADC=90°,得出△DQH是等腰直角三角形,由勾股定理得出结论.
| 1 |
| 3 |
(2)延长AE到Q,使EQ=FH,连接DQ,证△DFH≌△DEQ,推出DQ=DH,∠QDE=∠FDH,求出∠QDH=∠QDE+∠EDH=∠ADC=90°,得出△DQH是等腰直角三角形,由勾股定理得出结论.
解答:解:(1)∵DF=2,BE=DF,
∴BE=2,
∵四边形ABCD是正方形,
∴∠B=90°,
∵tan∠EAB=
,
∴AB=6,
∴AE=
=2
;
(2)证明:延长AE到Q,使EQ=FH,连接BQ,DH,
∵DC∥AB,
∴∠FGA=∠CFH,
∵∠FGA=∠BEA,∠AEB+∠BEQ=180°,
 ∴∠DFH=∠BEQ,
∴∠DFH=∠BEQ,
在△DFH和△BEQ中
,
∴△DFH≌△BEQ(SAS),
∴BQ=DH,∠QBE=∠FDH,
∵∠ADC=90°,
∴∠QDH=∠QDE+∠EDH=∠FDH+∠EDH=∠ADC=90°,
即△DQH是等腰直角三角形,
由勾股定理得:QH=
DH,
即EH+FH=
DH.
∴BE=2,
∵四边形ABCD是正方形,
∴∠B=90°,
∵tan∠EAB=
| 1 |
| 3 |
∴AB=6,
∴AE=
| 22+62 |
| 10 |
(2)证明:延长AE到Q,使EQ=FH,连接BQ,DH,
∵DC∥AB,
∴∠FGA=∠CFH,
∵∠FGA=∠BEA,∠AEB+∠BEQ=180°,
 ∴∠DFH=∠BEQ,
∴∠DFH=∠BEQ,在△DFH和△BEQ中
|
∴△DFH≌△BEQ(SAS),
∴BQ=DH,∠QBE=∠FDH,
∵∠ADC=90°,
∴∠QDH=∠QDE+∠EDH=∠FDH+∠EDH=∠ADC=90°,
即△DQH是等腰直角三角形,
由勾股定理得:QH=
| 2 |
即EH+FH=
| 2 |
点评:本题考查了正方形性质,全等三角形的性质和判定,等腰直角三角形的性质和判定以及勾股定理的运用,主要考查学生综合运用性质进行推理的能力,有一定的难度.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案
相关题目
下列计算正确的是( )
| A、m3-m2=m | ||
B、
| ||
| C、(m+n)2=m2+n2 | ||
| D、(m3)2=m6 |
袋子中装有5个红球、3个绿球,从袋子中随机摸出一个球,是绿球的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
二次函数y=
(x-6)2+3的顶点为( )
| 1 |
| 2 |
| A、(-6,3) |
| B、(6,3) |
| C、(-6,-3) |
| D、(6,-3) |