题目内容
19.如果将抛物线y=x2+2x-3向上平移,使它经过点A(0,2),那么所得新抛物线的表达式是y=x2+2x+2.分析 设平移后的抛物线解析式为y=x2+2x-3+b,把点A的坐标代入进行求值即可得到b的值.
解答 解:设平移后的抛物线解析式为y=x2+2x-3+b,
把A(0,2)代入,得
2=-3+b,
解得b=5.
则该函数解析式为y=x2+2x+2.
故答案是:y=x2+2x+2.
点评 主要考查了函数图象的平移,要求熟练掌握平移的规律:左加右减,上加下减.并用规律求函数解析式.会利用方程求抛物线与坐标轴的交点.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
7.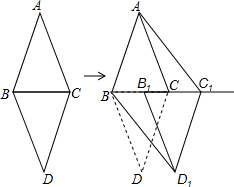 如图,△ABC和△DBC是两个具有公共边的全等三角形,AB=AC=6cm,BC=4cm,将△DBC沿射线BC平移一定的距离得到△D1B1C1,连接AC1,BD1.如果四边形ABD1C1是矩形,那么平移的距离为( )
如图,△ABC和△DBC是两个具有公共边的全等三角形,AB=AC=6cm,BC=4cm,将△DBC沿射线BC平移一定的距离得到△D1B1C1,连接AC1,BD1.如果四边形ABD1C1是矩形,那么平移的距离为( )
 如图,△ABC和△DBC是两个具有公共边的全等三角形,AB=AC=6cm,BC=4cm,将△DBC沿射线BC平移一定的距离得到△D1B1C1,连接AC1,BD1.如果四边形ABD1C1是矩形,那么平移的距离为( )
如图,△ABC和△DBC是两个具有公共边的全等三角形,AB=AC=6cm,BC=4cm,将△DBC沿射线BC平移一定的距离得到△D1B1C1,连接AC1,BD1.如果四边形ABD1C1是矩形,那么平移的距离为( )| A. | 14cm | B. | 16cm | C. | 18cm | D. | 20cm |
14.下列图形是轴对称而不是中心对称图形的是( )
| A. | 平行四边形 | B. | 菱形 | C. | 矩形 | D. | 等边三角形 |
9.已知点A(0,2),B(2,0),点C在y=x2的图象上,若△ABC的面积为$\frac{9}{4}$,则这样的C点有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
 如图,P为菱形ABCD的对角线上一点,PE丄AB于点E,PF丄AD于点F,PF=6
如图,P为菱形ABCD的对角线上一点,PE丄AB于点E,PF丄AD于点F,PF=6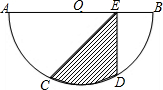 如图,AB为半圆O的直径,C、D是$\widehat{AB}$上的三等分点,若⊙O的半径为2,E是直径AB上任意一点,求图中阴影部分的面积.
如图,AB为半圆O的直径,C、D是$\widehat{AB}$上的三等分点,若⊙O的半径为2,E是直径AB上任意一点,求图中阴影部分的面积.