题目内容
13．“石油之光”是大庆市市标，如图，某兴趣小组利用课余时间研究市标的高度，在市标底部点A处沿着AC方向走到点B处，在点B处观察市标顶部，测得仰角为60°，继续沿AC方向走13米到点C处，在点C处测得仰角为45°，则市标AD的高度为30.7米（图中AD⊥AC，$\sqrt{2}≈1.41$，$\sqrt{3}≈1.73$，$\sqrt{5}≈2.24$，结果保留一位小数）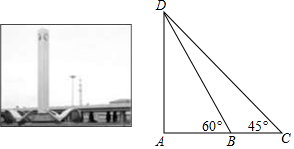
分析 由∠C=45°可设AD=AC=x米，则AB=（x-13）米，然后在Rt△ABD中，利用三角函数解答即可．
解答 解：∵∠C=45°，
设AD=AC=x米，则AB=（x-13）米，
在Rt△ABD中，$\frac{AD}{AB}$=tan60°，
∴$\frac{x}{x-13}$=$\sqrt{3}$，
解得x≈30.7，即市标AD的高度为30.7．
故答案为：30.7．
点评 本题考查了解直角三角形的应用-仰角俯角问题，熟练掌握等腰直角三角形的判定和性质、三角函数的定义是解题的关键．
练习册系列答案
相关题目
如图，点P将线段AB分割成两条线段AP、PB，且AP：AB=PB：AP，那么点P就叫做线段AB的黄金分割点；若AB=3，那么AP的长为$\frac{-3+3\sqrt{3}}{2}$．
如图，要利用一面墙（墙长为25米）建羊圈，用100米的围栏围成总面积为400平方米的三个大小相同的矩形羊圈，则羊圈的边长AB为20米．
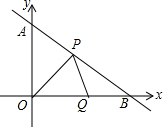如图，直线y=-$\frac{3}{4}$x+3与y轴交于点A，与x轴交于点B，点P从点B出发以每秒1个单位长度的速度沿BA边向终点A运动，同时点Q以相同的速度从坐标原点O出发沿OB边向终点B运动，设点P运动的时间为t秒．
2．线段CD是由线段AB平移得到的，点A（-2，-3）的对应点为C（3，1），则点B（-4，-1）的对应点D的坐标为（ ）
| A． | （1，3） | B． | （1，-5） | C． | （-9，-5） | D． | （-9，3） |
