题目内容
9. 如图,直线AB,CD相交于点O,OE⊥AB,∠COE=68°,则∠BOD等于22°.
如图,直线AB,CD相交于点O,OE⊥AB,∠COE=68°,则∠BOD等于22°.
分析 根据垂直的定义求得∠AOE=90°;然后根据余角的定义可以推知∠AOC=∠AOE-∠COE=22°;最后由对顶角的性质可以求得∠BOD=∠AOC=22°.
解答 解:∵OE⊥AB,
∴∠AOE=90°;
又∵∠COE=68°,
∴∠AOC=∠AOE-∠COE=22°,
∴∠BOD=∠AOC=22°(对顶角相等);
故答案是:22°.
点评 本题考查了垂线、对顶角与邻补角.注意,此题中隐含着已知条件“∠AOE=90°”.

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
19.(-2)2的算术平方根是( )
| A. | 2 | B. | ±2 | C. | 4 | D. | ±4 |
20.下列运算正确的是( )
| A. | (x2)3=x5 | B. | m5÷m2=m3 | C. | (a-b)2=a2-b2 | D. | m2•m3=m6 |
4.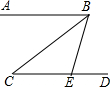 如图,AB∥CD,BC平分∠ABE,∠BED=72°,则∠C的度数是( )
如图,AB∥CD,BC平分∠ABE,∠BED=72°,则∠C的度数是( )
 如图,AB∥CD,BC平分∠ABE,∠BED=72°,则∠C的度数是( )
如图,AB∥CD,BC平分∠ABE,∠BED=72°,则∠C的度数是( )| A. | 28° | B. | 30° | C. | 36° | D. | 38° |
1.一组数据,6、4、a、3、5的平均数是5,这组数据的方差为( )
| A. | 10 | B. | 5 | C. | 3 | D. | 2 |
 如图,已知CD平分∠ACB,AE∥DC交BC的延长线于点E,若∠CAE=55°,则∠ACE=70°.
如图,已知CD平分∠ACB,AE∥DC交BC的延长线于点E,若∠CAE=55°,则∠ACE=70°. 在Rt△ABC中,∠C=90°,AC=6,BC=8,
在Rt△ABC中,∠C=90°,AC=6,BC=8,