题目内容
19．
在Rt△ABC中，∠C=90°，AC=6，BC=8，（1）用三角板作出斜边AB上的高．
（2）求斜边AB上的高．
分析 （1）直接利用三角形高线的作法得出即可；
（2）利用勾股定理得出AB的长，再利用直角三角形面积求出得出即可．
解答 
解：（1）如图所示：CD即为所求；
（2）∵在Rt△ABC中，∠C=90°，AC=6，BC=8，
∴AB=10，
由题意可得：CD×AB=AC×BC，
则10•CD=6×8，
解得：CD=4.8．
点评 此题主要考查了勾股定理以及直角三角形面积求法，正确掌握直角三角形的性质是解题关键．
练习册系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
如图，直线AB，CD相交于点O，OE⊥AB，∠COE=68°，则∠BOD等于22°．
7．
如图，函数y=3x与y=kx+b的图象交于点A（2，6），则不等式3x＜kx+b的解集为（ ）
如图，函数y=3x与y=kx+b的图象交于点A（2，6），则不等式3x＜kx+b的解集为（ ）| A． | x＜4 | B． | x＜2 | C． | x＞2 | D． | x＞4 |
14．
如图，矩形ABCD的对角线AC=5，则（ ）
如图，矩形ABCD的对角线AC=5，则（ ）| A． | AB=5 | B． | BC=5 | C． | CD=5 | D． | BD=5 |
4．
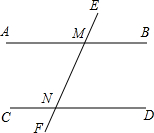如图，直线AB∥CD，EF分别交AB、CD于点M、N，若∠AME=125°，则∠CNF的度数为（ ）
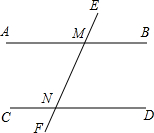如图，直线AB∥CD，EF分别交AB、CD于点M、N，若∠AME=125°，则∠CNF的度数为（ ）| A． | 125° | B． | 75° | C． | 65° | D． | 55° |
11．
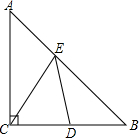如图所示，在△ABC中，∠ACB=90°，AC=BC=2，D是BC的中点，E是AB上的一动点，且不与A，B重合，是否存在一个位置，使DE+CE的值最小？若不存在，说明理由；若存在，试求出最小值．
如图所示，在△ABC中，∠ACB=90°，AC=BC=2，D是BC的中点，E是AB上的一动点，且不与A，B重合，是否存在一个位置，使DE+CE的值最小？若不存在，说明理由；若存在，试求出最小值．
15．
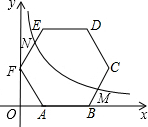如图，边长为4的正六边形ABCDEF的边AB在x轴上，顶点F在y轴上，点M是BC的中点，反比例函数y=$\frac{k}{x}$（k≠0，x＞0）的图象经过点M，且与正六边形交于另一点N，则点N的坐标是（ ）
如图，边长为4的正六边形ABCDEF的边AB在x轴上，顶点F在y轴上，点M是BC的中点，反比例函数y=$\frac{k}{x}$（k≠0，x＞0）的图象经过点M，且与正六边形交于另一点N，则点N的坐标是（ ）| A． | （$\frac{7}{4}\sqrt{3}，4$） | B． | （$\frac{7}{4}，4\sqrt{3}$） | C． | （2$\sqrt{2}-1，2\sqrt{6}+\sqrt{3}$） | D． | （2$\sqrt{2}+1，2\sqrt{6}-\sqrt{3}$） |