题目内容
已知数据x1、x2、x3、x4的标准差为3,则数据4x1+1、4x2+1、4x3+1、4x4+1的方差是 .
考点:方差,标准差
专题:
分析:已知x1、x2、x3、x4的标准差为3,则方差是9,根据方差的计算公式即可求得数据4x1+1、4x2+1、4x3+1、4x4+1的方差.
解答:解:设x1、x2、x3、x4的平均数是
,则数据4x1+1、4x2+1、4x3+1、4x4+1的平均数是4
+1,
∵数据x1、x2、x3、x4的标准差为3,
∴x1、x2、x3、x4的方差是9,
∴
[(x1-
)2+(x2-
)2+(x3-
)2+(x4-
)2]=9,
∴数据4x1+1、4x2+1、4x3+1、4x4+1的方差=
[(4x1+1-4
-1)2+(4x2+1-4
-1)2+(4x3+1-4
-1)2+(4x4+1-4
-1)2]
=16×
[(x1-
)2+(x2-
)2+(x3-
)2+(x4-
)2]
=16×9
=144.
故答案为144.
. |
| x |
. |
| x |
∵数据x1、x2、x3、x4的标准差为3,
∴x1、x2、x3、x4的方差是9,
∴
| 1 |
| 4 |
. |
| x |
. |
| x |
. |
| x |
. |
| x |
∴数据4x1+1、4x2+1、4x3+1、4x4+1的方差=
| 1 |
| 4 |
. |
| x |
. |
| x |
. |
| x |
. |
| x |
=16×
| 1 |
| 4 |
. |
| x |
. |
| x |
. |
| x |
. |
| x |
=16×9
=144.
故答案为144.
点评:本题考查了方差的定义:一般地,设n个数据,x1,x2,…xn的平均数为
,则S2=
[(x1-
)2+(x2-
)2+…+(xn-
)2],它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.同时考查了标准差:样本方差的算术平方根表示样本的标准差.
. |
| x |
| 1 |
| n |
. |
| x |
. |
| x |
. |
| x |

练习册系列答案
 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目
 如图,线段BD=
如图,线段BD= 如图,已知△ABC内接于⊙O,AE是⊙O的直径,AD⊥BC于D.求证:△ABE∽△ADC.
如图,已知△ABC内接于⊙O,AE是⊙O的直径,AD⊥BC于D.求证:△ABE∽△ADC.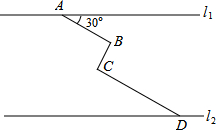 如图,在同一平面内,两条平行高速公路l1和l2间有一条“Z”型道路连通,其中AB段与高速公路l1成30°角,长为20km; BC段与AB、CD段都垂直,BC段长为10km,CD段长为30km.则两条高速公路l1和l2间的距离为
如图,在同一平面内,两条平行高速公路l1和l2间有一条“Z”型道路连通,其中AB段与高速公路l1成30°角,长为20km; BC段与AB、CD段都垂直,BC段长为10km,CD段长为30km.则两条高速公路l1和l2间的距离为