题目内容
10.在平面直角坐标系中,已知A(1,1)、B(3,5),要在x轴上找一点P,使得△PAB的周长最小,则点P的坐标为($\frac{4}{3}$,0).分析 因为AB的长度是确定的,故△PAB的周长最小就是PA+PB的值最小,因为3>5,所以点P在y轴上,作点A关于y轴的对称点A′,连接A′B交y轴于点P,求出P点坐标即可.
解答 解:∵线段AB的长度是确定的,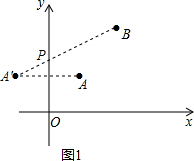 ∴△PAB的周长最小就是PA+PB的值最小,
∴△PAB的周长最小就是PA+PB的值最小,
∵3<5,
∴点P在y轴上,
如图1,作点A关于y轴的对称点A′,连接A′B交y轴于点P,
∵A(1,1),
∴A′(-1,1),
设直线A′B的解析式为y=kx+b(k≠0),
∴$\left\{\begin{array}{l}{3k+b=5}\\{-k+b=1}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=1\\;}\\{b=2}\end{array}\right.$,
∴直线A′B的解析式为y=x+2,
当x=0时,y=2,
∴P(0,2).
A′B=$\sqrt{{4}^{2}+{4}^{2}}=4\sqrt{2}$;
如图2,作点A关于x轴的对称点A′,连接A′B交y轴于点P,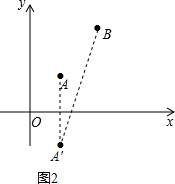 ∵A(1,1),
∵A(1,1),
∴A′(1,-1),
设直线A′B的解析式为y=kx+b(k≠0),
∴$\left\{\begin{array}{l}{3k+b=5}\\{k+b=-1}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=3}\\{b=-4}\end{array}\right.$,
∴直线A′B的解析式为y=3x-4,
当y=0时,x=$\frac{4}{3}$,
∴P($\frac{4}{3}$,0).
A′B=$\sqrt{{2}^{2}+{6}^{2}}=2\sqrt{10}$.
∵4$\sqrt{2}$<2$\sqrt{10}$.
故答案为:($\frac{4}{3}$,0)
点评 本题考查的是轴对称-最短路线问题,熟知“两点之间,线段最短”是解答此题的关键.

 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案| A. | y随x的增大而减小 | B. | y随x的增大而增大 | ||
| C. | 当x<0时,y随x的增大而减小 | D. | 图象在第二、四象限内 |
 已知:∠AOB=90°,∠EOF=90°,AO=BO,EO=FO,连结AE、BF.则AE与BF有什么关系,并说明理由.
已知:∠AOB=90°,∠EOF=90°,AO=BO,EO=FO,连结AE、BF.则AE与BF有什么关系,并说明理由.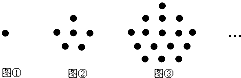 如图图形都是由同样大小的棋子按一定的规律组成,其中第①个图形有1颗棋子,第②个图形一共有6颗棋子,第③个图形一共有16颗棋子,…,则第⑧个图形中棋子的颗数为( )
如图图形都是由同样大小的棋子按一定的规律组成,其中第①个图形有1颗棋子,第②个图形一共有6颗棋子,第③个图形一共有16颗棋子,…,则第⑧个图形中棋子的颗数为( )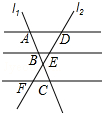 如图,AD∥BE∥CF,直线l1,l2与这三条平行线分别交于点A,B,C和点D,E,F,$\frac{AB}{BC}$=$\frac{2}{3}$,DE=6,则DF的值为( )
如图,AD∥BE∥CF,直线l1,l2与这三条平行线分别交于点A,B,C和点D,E,F,$\frac{AB}{BC}$=$\frac{2}{3}$,DE=6,则DF的值为( )