题目内容
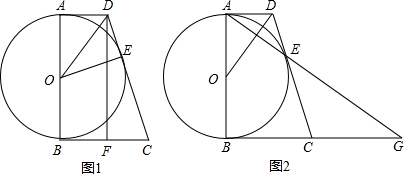
如图①,AB为⊙O的直径,AB=2
,AD与⊙O相切于点A,过点B作BC∥AD,DO平分∠ADC.
(1)判断DC与⊙O相切吗?并说明理由;
(2)设AD=x,BC=y,求y与x的函数关系式;
(3)若⊙O与直线DC相切,连接点A与切点E并延长交BC延长线于点G,当AD=2时,求线段EG的长.
| 5 |
(1)判断DC与⊙O相切吗?并说明理由;
(2)设AD=x,BC=y,求y与x的函数关系式;
(3)若⊙O与直线DC相切,连接点A与切点E并延长交BC延长线于点G,当AD=2时,求线段EG的长.

考点:圆的综合题
专题:
分析:(1)可作OE⊥DC,要证DC与⊙O相切,只要证出AO=OE即可,运用角的平分线的性质可证出AO=OE.
(2)由切线性质可得出DC的关系式,再由DF⊥BC,可得四边形ABFD是矩形,从而得出DF、FC,在Rt△DFC中,可运用勾股定理求出y与x的函数关系式.
(3)由⊙O与直线DC相切,利用(2)中的函数关系式求出CG,再在Rt△ABG中,运用勾股定理求出AG,再运用△ADE∽△GCE列出比例式,即可求出EG的长.
(2)由切线性质可得出DC的关系式,再由DF⊥BC,可得四边形ABFD是矩形,从而得出DF、FC,在Rt△DFC中,可运用勾股定理求出y与x的函数关系式.
(3)由⊙O与直线DC相切,利用(2)中的函数关系式求出CG,再在Rt△ABG中,运用勾股定理求出AG,再运用△ADE∽△GCE列出比例式,即可求出EG的长.
解答:
解:(1)如图1,作OE⊥DC.
∵AD与⊙O相切
∴AD⊥AB
∴∠A=90°
∵DO平分∠ADC
且AD⊥AB,OE⊥DC
∴OE=AO=r
∴DC与⊙O相切
(2)如图1,作DF⊥BC

∵BC∥AD
∴∠B=90°
∴BC与⊙O相切
∵AD与⊙O相切,DC与⊙O相切
∴AD=DE
同理得:BC=CE
∴DC=DE+EC=AD+BC=x+y
∵DF⊥BC
∴∠DFB=90°
∵∠A=90°,∠B=90°,∠DFB=90°
∴四边形ABFD是矩形
∴DF=AB=2
,FC=BC-AD=y-x
在Rt△DFC中,DC2=DF2+FC
∴(x+y)2=(y-x)2+(2
)
∴y=
,
(3)如图2,

∵AD=DE
∴∠DAE=∠DEA
∵BG∥AD
∴∠DAE=∠G
∵∠CEG=∠DEA
∴∠CEG=∠G
∴EC=CG
∵AD=2
∴由(2)得BC=EC=CG=2.5
在Rt△ABG中,AG2=AB2+BG2,
∴AG=3
,
∵BG∥AD
∴△ADE∽△GCE
∴
=
,即
=
∴EG=
.

解:(1)如图1,作OE⊥DC.
∵AD与⊙O相切
∴AD⊥AB
∴∠A=90°
∵DO平分∠ADC
且AD⊥AB,OE⊥DC
∴OE=AO=r
∴DC与⊙O相切
(2)如图1,作DF⊥BC

∵BC∥AD
∴∠B=90°
∴BC与⊙O相切
∵AD与⊙O相切,DC与⊙O相切
∴AD=DE
同理得:BC=CE
∴DC=DE+EC=AD+BC=x+y
∵DF⊥BC
∴∠DFB=90°
∵∠A=90°,∠B=90°,∠DFB=90°
∴四边形ABFD是矩形
∴DF=AB=2
| 5 |
在Rt△DFC中,DC2=DF2+FC
∴(x+y)2=(y-x)2+(2
| 5 |
∴y=
| 5 |
| x |
(3)如图2,

∵AD=DE
∴∠DAE=∠DEA
∵BG∥AD
∴∠DAE=∠G
∵∠CEG=∠DEA
∴∠CEG=∠G
∴EC=CG
∵AD=2
∴由(2)得BC=EC=CG=2.5
在Rt△ABG中,AG2=AB2+BG2,
∴AG=3
| 5 |
∵BG∥AD
∴△ADE∽△GCE
∴
| AD |
| CG |
| AE |
| EG |
| 2 |
| 2.5 |
3
| ||
| EG |
∴EG=
5
| ||
| 3 |
点评:本题主要考查了圆的综合题,解题的关键是运用切线的性质及勾股定理求线段.

练习册系列答案
相关题目