题目内容
8.如图,在由边长为1的小正方形组成的网格中建立平面直角坐标系xOy,点A的坐标是(3,1),连接OA.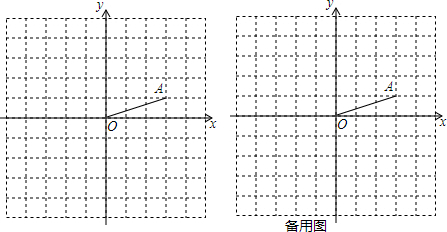
(1)线段OA的垂直平分线与x轴交点的横坐标是$\frac{5}{3}$;
(2)在网格中用2B铅笔画出线段OA绕点O逆时针方向旋转90°后的对应线段OB,连接AB,求AB的长;
(3)在(2)的条件下,若△A′OB′与△AOB位似,点O是位似中心,点A的对应点是点A′,且A′B′=$\sqrt{5}$,则点A′的坐标是($\frac{3}{2}$,$\frac{1}{2}$)或(-$\frac{3}{2}$,-$\frac{1}{2}$).
分析 (1)利用勾股定理得出AO的长,再利用锐角三角函数关系得出DO的长;
(2)利用旋转的性质得出B点位置进而得出AB的长;
(3)利用位似图形的性质,得出点A′的坐标有2个.
解答  解:(1)作OA的垂直平分线CD,交x轴于点D,
解:(1)作OA的垂直平分线CD,交x轴于点D,
∵AO=$\sqrt{{3}^{2}+{1}^{2}}$=$\sqrt{10}$,则OC=$\frac{\sqrt{10}}{2}$,
故cos∠AOD=$\frac{OC}{OD}$=$\frac{3}{\sqrt{10}}$=$\frac{\frac{\sqrt{10}}{2}}{DO}$,
解得:OD=$\frac{5}{3}$,
则线段OA的垂直平分线与x轴交点的横坐标是:$\frac{5}{3}$;
故答案为:$\frac{5}{3}$;
(2)如图所示:
∵OA=$\sqrt{10}$,
在△ABO中,∠AOB=90°,AO=BO,
由勾股定理得:AB2=AO2+BO2=20,
则AB=2$\sqrt{5}$;
(3)∵△A′OB′与△AOB位似,点O是位似中心,点A的对应点是点A′,且A′B′=$\sqrt{5}$,
∴$\frac{A′B′}{AB}$=$\frac{\sqrt{5}}{2\sqrt{5}}$=$\frac{1}{2}$,
则点A′的坐标是:($\frac{3}{2}$,$\frac{1}{2}$)或(-$\frac{3}{2}$,-$\frac{1}{2}$).
故答案为:($\frac{3}{2}$,$\frac{1}{2}$)或(-$\frac{3}{2}$,-$\frac{1}{2}$).
点评 此题主要考查了旋转变换以及位似变换的性质,正确掌握位似图形的性质是解题关键.

练习册系列答案
相关题目
13.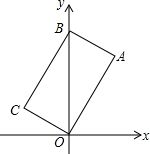 矩形OABC在如图所示的平面直角坐标系中,点B的坐标是(0,2),∠AOB=30°,则点C的坐标是( )
矩形OABC在如图所示的平面直角坐标系中,点B的坐标是(0,2),∠AOB=30°,则点C的坐标是( )
 矩形OABC在如图所示的平面直角坐标系中,点B的坐标是(0,2),∠AOB=30°,则点C的坐标是( )
矩形OABC在如图所示的平面直角坐标系中,点B的坐标是(0,2),∠AOB=30°,则点C的坐标是( )| A. | (-$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$) | B. | (-$\frac{\sqrt{3}}{2}$,$\frac{1}{2}$) | C. | (-$\sqrt{3}$,1) | D. | (-1,$\sqrt{3}$) |
20.下列计算正确的是( )
| A. | 2$\sqrt{\frac{1}{2}}$=$\sqrt{2}$ | B. | $\sqrt{2}$$+\sqrt{3}$=$\sqrt{5}$ | C. | 4$\sqrt{3}$-3$\sqrt{3}$=1 | D. | 3+2$\sqrt{2}$=5$\sqrt{2}$ |
 如图,某校A位于工地O的正西方向,且OA=200m,一辆红岩大货车从O点出发,以每秒10米的速度沿北偏西53°方向行驶,已知货车的噪声污染半径为130m,则学校受噪声污染的时间为10秒.(已知sin53°=0.80,tan37°=0.75)
如图,某校A位于工地O的正西方向,且OA=200m,一辆红岩大货车从O点出发,以每秒10米的速度沿北偏西53°方向行驶,已知货车的噪声污染半径为130m,则学校受噪声污染的时间为10秒.(已知sin53°=0.80,tan37°=0.75)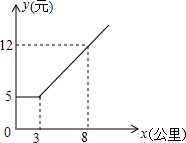 某市出租车公司收费标准如图所示,x(公里)表示行驶里程,y(元)表示车费,请根据图象回答下面的问题:
某市出租车公司收费标准如图所示,x(公里)表示行驶里程,y(元)表示车费,请根据图象回答下面的问题: