题目内容
已知α+β=90°，且sinα+cosβ-
=0，则锐角α等于（ ）
| 3 |
| A、30° | B、45° |
| C、60° | D、无法求 |
考点：特殊角的三角函数值,互余两角三角函数的关系
专题：
分析：根据互余两角的三角函数的关系得出cosβ=sinα，求出sinα=
，即可得出答案．
| ||
| 2 |
解答：解：∵α+β=90°，
∴cosβ=sinα，
∵sinα+cosβ-
=0，
2sinα-
=0，
sinα=
，
锐角α=60°．
故选C．
∴cosβ=sinα，
∵sinα+cosβ-
| 3 |
2sinα-
| 3 |
sinα=
| ||
| 2 |
锐角α=60°．
故选C．
点评：本题考查了互余两角的三角函数的关系，特殊角的三角函数值的应用，解此题的关键是求出sinα的值．
练习册系列答案
相关题目
如图在Rt△ABC中，∠ACB=90°，CD⊥AB于D．
如图，⊙O中，半径OC⊥弦AB，∠BAC=20°，则∠AOC的度数是（ ）| A、30° | B、40° |
| C、50° | D、60° |
如图，在△ABC中，∠B与∠C的平分线交于点O，过点O作DE∥BC，分别交AB、AC于点D、E．若AB=5，AC=3，则△ADE的周长是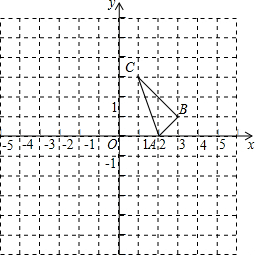
如图所示的正方形网格中，△ABC的顶点均在格点上，在所给平面直角坐标系中解答下列问题：