题目内容
1．
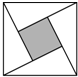“赵爽弦图”是四个全等的直角三角形与中间一个小正方形拼成的大正方形，如图，其直角三角形的两条直角边的长分别是2和4，则小正方形与大正方形的面积比是（ ）| A． | 1：2 | B． | 1：4 | C． | 1：5 | D． | 1：10 |
分析 根据题意求得小正方形的边长，根据勾股定理求出大正方形的边长，由正方形的面积公式即可得出结果．
解答 解：∵直角三角形的两条直角边的长分别是2和4，
∴小正方形的边长为2，
根据勾股定理得：大正方形的边长=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$，
∴$\frac{小正方形面积}{大正方形面积}$=$\frac{{2}^{2}}{（2\sqrt{5}）^{2}}$=$\frac{4}{20}$=$\frac{1}{5}$．
故选：C．
点评 本题考查了勾股定理和正方形的面积．本题是用数形结合来证明勾股定理，锻炼了同学们的数形结合的思想方法．
练习册系列答案
习题精选系列答案
相关题目
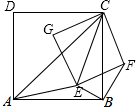如图，已知AC，EC分别为正方形ABCD和正方形EFCG的对角线，点E在△ABC内，连接BF，∠CAE+∠CBE=90°．
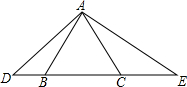如图，等边三角形ABC中，D为CB延长线上一点，E为BC延长线上点，且满足∠DAE=120°．
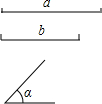如图，已知线段a、b和∠α，用尺规作一个三角形ABC，使BC=a，AC=b，∠ACB=∠α（要求：不写已知、求作、作法、只画图，保留作图痕迹）