题目内容
1．
如图，将△ABC的∠A沿DE折叠，探索∠1，∠2，∠A之间的数量关系2∠A=∠1-∠2．
分析 根据折叠可知∠A与∠A′是相等的，再两次运用三角形外角的性质可得结论2∠A=∠1-∠2．
解答 
解：如图，设DA′交AC于点F．
∵∠1=∠A+∠DFA，∠DFA=∠A′+∠2，
∴∠1=∠A+∠A′+∠2，
∴∠A+∠A′=∠1-∠2，
∵△A′DE是由△ADE沿直线DE折叠而得，
∴∠A=∠A′，
∴2∠A=∠1-∠2，
故答案为2∠A=∠1-∠2．
点评 此题主要考查了三角形内角和定理以及翻折变换的性质，遇到折叠的问题，一定要找准相等的量，结合题目所给出的条件在图形上找出之间的联系则可．
练习册系列答案
备战中考寒假系列答案
相关题目
己知：如图，在梯形ABCD中，点E、F分别在AB、CD上，AD∥EF∥BC，CE平分∠BCD，AE：EB=1：2，AD=4，BC=10，求CD的长．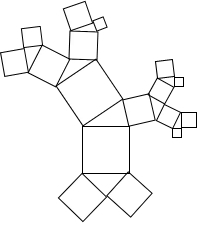
如图，美丽的珊瑚礁图案中，所有的四边形都是正方形，所有的三角形都是直角三角形．所有正方形（包括最大的正方形）的面积之和为500cm2，最大的正方形边长为10．
在比赛中，某次羽毛球的运动路线可以看作是抛物线y=-$\frac{1}{4}$x2+bx+c的一部分，如图，其中出球点B离地面O点的距离是1m，球落地点A到O点的距离是4m，求这条抛物线的解析式和羽毛球飞行的最大高度．
观察图，先填空，然后回答问题：
如图，在?ABCD中，∠A-∠B=40°，则∠A=110°．
已知一个由50个偶数排成的数阵，请你观察框内的四个数之间的关系并解答下列问题：在数阵中任意作一个类似图中的框．
已知：如图，把长方形纸片ABCD沿EF折叠后，点D与点B重合，点C落在点C'的位置上，若∠1=60°，AE=1．