题目内容
求下列各式中x的值
(1)5x2-10=0
(2)25(x+2)2-49=0
(3)(2x)3=-8
(4)-(x-3)3=27.
解:(1)∵x2=2,
∴x=± ;
;
(2)∵(x+2)2= ,
,
∴x+2=± ,
,
∴x=- 或-
或- ;
;
(3)∵2x=-2,
∴x=-1;
(4)∵(x-3)3=-27,
∴x-3=-3,
∴x=0.
分析:(1)移项后等式两边都除以5得到x2=2,然后根据平方根的定义求解;
(2)移项后等式两边都除以25得到(x+2)2= ,然后根据平方根的定义得到两个一元一次方程x+2=±
,然后根据平方根的定义得到两个一元一次方程x+2=± ,再解方程即可;
,再解方程即可;
(3)根据立方根的定义得到2x=-2,然后解一元一次方程即可;
(3)两边都乘以-1得到(x-3)3=-27,根据立方根的定义得到x-3=-3,再解一元一次方程即可.
点评:本题考查了立方根:若一个数的立方等于a,那么这个数叫a的立方根,记作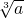 .也考查了平方根的定义.
.也考查了平方根的定义.
∴x=±
 ;
;(2)∵(x+2)2=
 ,
,∴x+2=±
 ,
,∴x=-
 或-
或- ;
;(3)∵2x=-2,
∴x=-1;
(4)∵(x-3)3=-27,
∴x-3=-3,
∴x=0.
分析:(1)移项后等式两边都除以5得到x2=2,然后根据平方根的定义求解;
(2)移项后等式两边都除以25得到(x+2)2=
 ,然后根据平方根的定义得到两个一元一次方程x+2=±
,然后根据平方根的定义得到两个一元一次方程x+2=± ,再解方程即可;
,再解方程即可;(3)根据立方根的定义得到2x=-2,然后解一元一次方程即可;
(3)两边都乘以-1得到(x-3)3=-27,根据立方根的定义得到x-3=-3,再解一元一次方程即可.
点评:本题考查了立方根:若一个数的立方等于a,那么这个数叫a的立方根,记作
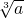 .也考查了平方根的定义.
.也考查了平方根的定义. 
练习册系列答案
相关题目