题目内容
如图，在△ABC中，AC⊥BC，∠B=15°，AD=BD，AC=1，求△ABC的面积．考点：勾股定理,含30度角的直角三角形
专题：
分析：在Rt△ADC中，求出AD的长，求出DC的长，根据AD=BD，求出BD的长，从而得到BC=BD+DC．
解答：解：∵AD=BD，
∴∠B=∠BAD=15°，
∴∠ADB=180°-∠B-∠BAD=180°-15°-15°=150°，
∴∠ADC=30°，
又∵AC⊥BC，
∴在Rt△ADC中，AD=2AC=2×1=2，
∵DC2+AC2=AD2，
∴DC2=22-12=3，
∴DC=
，
∴BC=BD+DC=2+
，
∴S△ABC=
BC•AC=
×（2+
）×1=
．
∴∠B=∠BAD=15°，
∴∠ADB=180°-∠B-∠BAD=180°-15°-15°=150°，
∴∠ADC=30°，
又∵AC⊥BC，
∴在Rt△ADC中，AD=2AC=2×1=2，
∵DC2+AC2=AD2，
∴DC2=22-12=3，
∴DC=
| 3 |
∴BC=BD+DC=2+
| 3 |
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
2+
| ||
| 2 |
点评：本题考查了勾股定理、含30°角的直角三角形，熟悉勾股定理是解题的关键．
练习册系列答案
相关题目
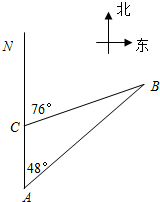如图，一艘货轮以30海里/时的速度在海面上航行，当它行驶到A处时，发现在它的北偏东48°方向有一港口B，货轮继续向北航行40分钟后到达C处，发现港口B在它的北偏东76°方向上，若货轮急需到港口B补充供给，请求出C处与港口B的距离CB的长度．（结果保留整数）
如图所示，河堤横断面迎水坡AB的坡比是1：3，堤高BC=5m，则坡面AB的长度是