Question

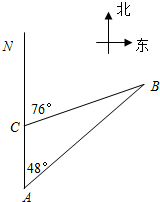如图，一艘货轮以30海里/时的速度在海面上航行，当它行驶到A处时，发现在它的北偏东48°方向有一港口B，货轮继续向北航行40分钟后到达C处，发现港口B在它的北偏东76°方向上，若货轮急需到港口B补充供给，请求出C处与港口B的距离CB的长度．（结果保留整数）
（参考数据：sin76°≈

20

21

，tan76°≈4，tan48°≈

10

9

，sin48°≈

4

5

）

Answer 1

考点：解直角三角形的应用-方向角问题

专题：

分析：在Rt△BDC中，

BD

CD

=tan76°，则BD=CD•tan76°，在Rt△ABD中，求出CD，在Rt△BDC中，求出BD，从而得到BC的长．

解答：解：AC=30×

40

60

=20海里，
在Rt△BDC中，

BD

CD

=tan76°，
则BD=CD•tan76°，
在Rt△ABD中，

BD

AD

=tan48°，
即

CD•tan76°

20+CD

=tan48°，
于是

4CD

20+CD

=

10

9

，
解得CD=

100

13

，
BD=

100

13

×4=

400

13

，
在Rt△BDC中，

BD

CB

=sin76°，

400 13

BC

=

20

21

，
则BC≈32海里．

点评：本题考查了解直角三角形的应用--方向角问题，灵活运用三角函数是解题的关键．