题目内容
 如图,AB是⊙0的弦,P为AB上一点,AB=8cm,PA=2cm,OP=3cm,求⊙0的半径.
如图,AB是⊙0的弦,P为AB上一点,AB=8cm,PA=2cm,OP=3cm,求⊙0的半径.考点:垂径定理,勾股定理
专题:计算题
分析:过O作OE⊥AB,垂足为E,连接OA,先求出PE的长,利用勾股定理求出OE,在Rt△AOE中,利用勾股定理即可求出OA的长.
解答:解:过O作OE⊥AB,垂足为E,连接OA,
∵AB=8cm,PA=2cm,
∴AE=
AB=4cm,PE=AE-PA=4cm-2cm=2cm,
在Rt△POE中,OE=
=
=
(cm),
在Rt△AOE中,OA=
=
=
(cm),
即⊙0的半径是
cm.
答:⊙0的半径为
cm.

∵AB=8cm,PA=2cm,
∴AE=
| 1 |
| 2 |
在Rt△POE中,OE=
| OP2-PE2 |
| 32-22 |
| 5 |
在Rt△AOE中,OA=
| AE2+OE2 |
42+(
|
| 21 |
即⊙0的半径是
| 21 |
答:⊙0的半径为
| 21 |
点评:本题主要考查垂径定理和勾股定理的应用.作辅助线构造直角三角形是解题的突破口.

练习册系列答案
相关题目
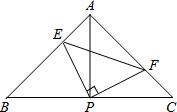 如图,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE、PF分别交AB、AC于点E、F,给出以下四个结论:
如图,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE、PF分别交AB、AC于点E、F,给出以下四个结论:
 已知A,B,C,D,E各点的坐标如图,请分别求出△ABC、△EAB和△BDE的面积.
已知A,B,C,D,E各点的坐标如图,请分别求出△ABC、△EAB和△BDE的面积. 如图,直线PQ、MN被直线EF所截,交点分别为A、C,AB平分∠EAQ,CD平分∠ACN,如果PQ∥MN,那么AB与CD平行吗?为什么?
如图,直线PQ、MN被直线EF所截,交点分别为A、C,AB平分∠EAQ,CD平分∠ACN,如果PQ∥MN,那么AB与CD平行吗?为什么? 如图,已知△ABC中,AB=AC=10cm,BC=8cm,点D为AB的中点.如果点P在线段BC上以3cm/s的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.
如图,已知△ABC中,AB=AC=10cm,BC=8cm,点D为AB的中点.如果点P在线段BC上以3cm/s的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.