题目内容
(1)在Rt△ABC中,∠C=90°,∠A的正弦、余弦之间有什么关系?请给出证明过程.
(2)已知锐角α满足:sinα=1-x,cosα=1-2x,求tanα的值.
(2)已知锐角α满足:sinα=1-x,cosα=1-2x,求tanα的值.
考点:同角三角函数的关系
专题:
分析:(1)利用正弦与余弦的定义及勾股定理得到同角的正弦与余弦之间的关系;
(2)利用上题证得的关系式代入求解即可.
(2)利用上题证得的关系式代入求解即可.
解答:解:(1)∵Rt△ABC中,∠C=90°,
∴a2+b2=c2
∵sinA=
cosA=
∴sin2A+cos2A=(
)2+(
)2=
=
=1
故sin2A+cos2A=1
(2)由sin2α+cos2α=1,得(1-x)2+(1-2x)2=1,
解得x=
或x=1(舍)
∴tanα=
=
=
=
=
.
∴a2+b2=c2
∵sinA=
| a |
| c |
| b |
| c |
∴sin2A+cos2A=(
| a |
| c |
| b |
| c |
| a2+b2 |
| c2 |
| c2 |
| c2 |
故sin2A+cos2A=1
(2)由sin2α+cos2α=1,得(1-x)2+(1-2x)2=1,
解得x=
| 1 |
| 5 |
∴tanα=
| a |
| b |
| ||
|
| sinα |
| cosα |
| ||
|
| 4 |
| 3 |
点评:本题考查了同角的三角函数的关系,解题的关键是熟记各个锐角三角函数之间的关系.

练习册系列答案
 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
设一个凸多边形的边数为奇数,除去两个内角外,其余内角和为2390°,则除去的这两内角的度数和为( )
| A、130° | B、300° |
| C、310° | D、490° |
要使式子
有意义,则x的取值范围是( )
| x | ||
|
| A、x≥-3且x≠0 |
| B、.x≥-3 |
| C、x>-3 |
| D、全体实数 |
某段公路由上坡、平坡、下坡三个等长的路段组成,已知一辆汽车在三个路段上行驶的平均速度分别为v1,v2,v3,则此辆汽车在这段公路上行驶的平均速度为( )
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
 如图,E、F是平行四边形ABCD对角线AC上的两点,且BE∥DF.求证:∠1=∠2.
如图,E、F是平行四边形ABCD对角线AC上的两点,且BE∥DF.求证:∠1=∠2.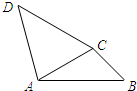 如图,在四边形ABCD中,∠ACB=∠BAD=105°,∠ABC=∠ADC=45°,若AB=2,则CD的长为
如图,在四边形ABCD中,∠ACB=∠BAD=105°,∠ABC=∠ADC=45°,若AB=2,则CD的长为