题目内容
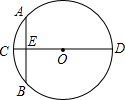 “圆材埋壁”是我国古代数一学著作《九章算术》中的一个问题.“今有圆材,埋壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”用现在的数学语言表达是:如图所示,CD为⊙O的直径,弦AB⊥CD,垂足为E,CE=1寸,AB=1尺,则直径CD长为
“圆材埋壁”是我国古代数一学著作《九章算术》中的一个问题.“今有圆材,埋壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”用现在的数学语言表达是:如图所示,CD为⊙O的直径,弦AB⊥CD,垂足为E,CE=1寸,AB=1尺,则直径CD长为考点:垂径定理的应用,勾股定理
专题:计算题
分析:连接OA,设OA=r,则OE=r-CE=r-1,再根据垂径定理求出AE的长,在Rt△OAE中根据勾股定理求出r的值,进而得出结论.
解答: 解:连接OA,设OA=r,则OE=r-CE=r-1,
解:连接OA,设OA=r,则OE=r-CE=r-1,
∵AB⊥CD,AB=1尺,
∴AE=
AB=5寸,
在Rt△OAE中,
OA2=AE2+OE2,即r2=52+(r-1)2,
解得r=13(寸).
∴CD=2r=26寸.
故答案为:26.
 解:连接OA,设OA=r,则OE=r-CE=r-1,
解:连接OA,设OA=r,则OE=r-CE=r-1,∵AB⊥CD,AB=1尺,
∴AE=
| 1 |
| 2 |
在Rt△OAE中,
OA2=AE2+OE2,即r2=52+(r-1)2,
解得r=13(寸).
∴CD=2r=26寸.
故答案为:26.
点评:本题考查的是垂径定理的应用,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
如图是小兵一天上学、放学时看到的一根电线杆的影子的俯视图,将它们按时间先后顺序进行排列,排列正确的是( )
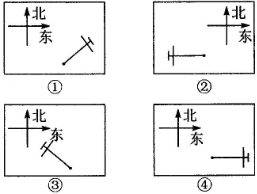

| A、①②③④ | B、②③④① |
| C、②③①④ | D、③①④② |
 看图填空.
看图填空. 如图,该图形至少绕圆心旋转
如图,该图形至少绕圆心旋转 如图,在等腰△ABC中,AB=AC,PM,QN分别是AB,AC的垂直平分线,∠BAC=110°,则∠PAQ的度数为
如图,在等腰△ABC中,AB=AC,PM,QN分别是AB,AC的垂直平分线,∠BAC=110°,则∠PAQ的度数为 如图,已知△ABC的周长为a,A1B1,B1C1,A1C1是△ABC的三条中位线,它们构成了△A1B1C1,△A2B2C2是由△A1B1C1的三条中位线A2B2,B2C2,A2C2构成的…如此进行下去得到△AnBnCn,则△A1B1C1的周长为
如图,已知△ABC的周长为a,A1B1,B1C1,A1C1是△ABC的三条中位线,它们构成了△A1B1C1,△A2B2C2是由△A1B1C1的三条中位线A2B2,B2C2,A2C2构成的…如此进行下去得到△AnBnCn,则△A1B1C1的周长为 如图,△ABC的三边分别切⊙O于点D,E,F.若AB=7,BC=8,AC=9,则BE=
如图,△ABC的三边分别切⊙O于点D,E,F.若AB=7,BC=8,AC=9,则BE=