题目内容
完成下列证明:
当p1•p2=2(q1+q2)时,求证:方程x2+p1x+q1=0和方程x2+p2x+q2=0中,至少有一个方程有实数根.
证明:假设 ,那么△1=p12-4q1 0,△2=
-4q2 0.
∴p12 4q1,
4q2,
∴p12+
4(q1+q2) 2p1p2,
∴(p1-p2)2 0,这与(p1-p2)2 0相矛盾.
∴假设 不成立,故所求证的结论正确.
当p1•p2=2(q1+q2)时,求证:方程x2+p1x+q1=0和方程x2+p2x+q2=0中,至少有一个方程有实数根.
证明:假设
| p | 2 2 |
∴p12
| p | 2 2 |
∴p12+
| p | 2 2 |
∴(p1-p2)2
∴假设
考点:反证法
专题:
分析:至少有一个方程有实根的对立面是两个方程都没有根,由于正面解决此问题分类较多,而其对立面情况单一,故求解此类问题一般先假设所有方程都有实数根,然后由根的判别式解得方程都没有实数根得(p1-p2)2 的取值范围,进而得出矛盾,原命题正确.
解答:证明:假设方程x2+p1x+q1=0和方程x2+p2x+q2=0中都没有实数根,
那么△1=p12-4q1<0,△2=
-4q2<0.
∴p12<4q1,
<4q2,
∴p12+
<4(q1+q2)<2p1p2,
∴(p1-p2)2<0,这与(p1-p2)2<0相矛盾.
∴假设方程x2+p1x+q1=0和方程x2+p2x+q2=0中都没有实数根不成立,故所求证的结论正确.
那么△1=p12-4q1<0,△2=
| p | 2 2 |
∴p12<4q1,
| p | 2 2 |
∴p12+
| p | 2 2 |
∴(p1-p2)2<0,这与(p1-p2)2<0相矛盾.
∴假设方程x2+p1x+q1=0和方程x2+p2x+q2=0中都没有实数根不成立,故所求证的结论正确.
点评:本题考查了反证法,解此题关键要懂得反证法的意义及步骤.在假设结论不成立时要注意考虑结论的反面所有可能的情况,如果只有一种,那么否定一种就可以了,如果有多种情况,则必须一一否定.

练习册系列答案
相关题目
下列各式中,两式相乘得x2-5x-6的是( )
| A、(x-2)(x-3) |
| B、(x-1)(x+6) |
| C、(x-6)(x+1) |
| D、(x+2)(x+3) |
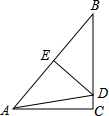 如图,在△ABC中,∠C=90°,DE是AB的垂直平分线.
如图,在△ABC中,∠C=90°,DE是AB的垂直平分线.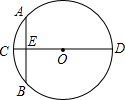 “圆材埋壁”是我国古代数一学著作《九章算术》中的一个问题.“今有圆材,埋壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”用现在的数学语言表达是:如图所示,CD为⊙O的直径,弦AB⊥CD,垂足为E,CE=1寸,AB=1尺,则直径CD长为
“圆材埋壁”是我国古代数一学著作《九章算术》中的一个问题.“今有圆材,埋壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”用现在的数学语言表达是:如图所示,CD为⊙O的直径,弦AB⊥CD,垂足为E,CE=1寸,AB=1尺,则直径CD长为