题目内容
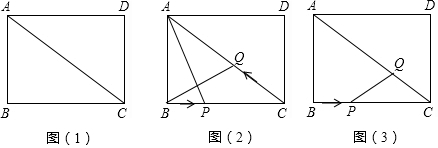
6.我们规定:在正方形ABCD中,以正方形的一个顶点A为顶点,且过对角顶点C的抛物线,称为这个正方形的以A为顶点的对角抛物线.(1)在平面直角坐标系xOy中,点在轴正半轴上,点C在y轴正半轴上.
①如图1,正方形OABC的边长为2,求以O为顶点的对角抛物线;
②如图2,在平面直角坐标系xOy中,正方形OABC的边长为a,其以O为顶点的对角抛物线的解析式为y=$\frac{1}{4}$x2,求a的值;
(2)如图3,正方形ABCD的边长为4,且点A的坐标为(3,2),正方形的四条对角抛物线在正方形ABCD内分别交于点M、P、N、Q,直接写出四边形MPNQ的形状和四边形MPNQ的对角线的交点坐标.
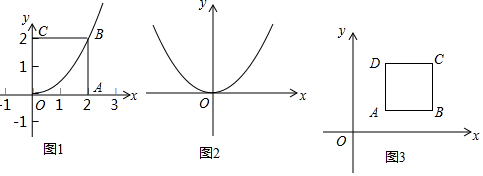
分析 (1)①设O为顶点的抛物线的解析式为y=ax2,把B(2,2)代入即可解决问题.
②设B(a,a).代入y=$\frac{1}{4}$x2求出a即可解决问题.
(2)如图3中,结论:四边形MPNQ是菱形,对角线的交点坐标为(5,4).求出A、B、C、D的顶点的对角抛物线,利用方程组求出M、P、N、Q的坐标即可解决问题.
解答 解:(1)①如图1中,设O为顶点的抛物线的解析式为y=ax2,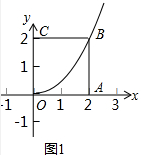
∵过B(2,2),
∴2=4a,
∴a=$\frac{1}{2}$,
∴所求的抛物线的解析式为y=$\frac{1}{2}$x2.
②如图2中,设B(a,a).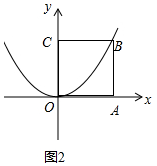
则有a=$\frac{1}{4}$a2,解得a=4或0(舍弃),
∴B(4,4),
∴OA=4,
∴正方形的边长为4.
(2)如图3中,结论:四边形MPNQ是菱形,对角线的交点坐标为(5,4).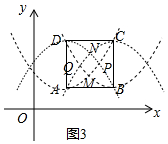
理由:∵正方形ABCD的边长为4,A(3,2),
∴B(7,2),C(7,6),D(3,6),
∴以A为顶点的对角抛物线为y=$\frac{1}{4}$(x-3)2+2,
以B为顶点的对角抛物线为y=$\frac{1}{4}$(x-7)2+2,
以C为顶点的对角抛物线为y=-$\frac{1}{4}$(x-7)2+6,
以D为顶点的对角抛物线为y=-$\frac{1}{4}$(x-3)2+6,
由$\left\{\begin{array}{l}{y=\frac{1}{4}(x-3)^{2}+2}\\{y=\frac{1}{4}(x-7)^{2}+2}\end{array}\right.$可得M(5,3),
由$\left\{\begin{array}{l}{y=-\frac{1}{4}(x-7)^{2}+6}\\{y=-\frac{1}{2}(x-3)^{2}+6}\end{array}\right.$可得N(5,5),
由$\left\{\begin{array}{l}{y=\frac{1}{4}(x-3)^{2}+2}\\{Y=-\frac{1}{4}(x-3)^{2}+6}\end{array}\right.$可得P(3+2$\sqrt{2}$,4),
由$\left\{\begin{array}{l}{y=\frac{1}{4}(x-7)^{2}+2}\\{y=-\frac{1}{4}(x-7)^{2}+6}\end{array}\right.$可得Q(7-2$\sqrt{2}$,4),
∴PM=$\sqrt{(2\sqrt{2}-2)^{2}+{1}^{2}}$,
PN=$\sqrt{(2\sqrt{2}-2)^{2}+{1}^{2}}$,
QN=$\sqrt{(2\sqrt{2}-2)^{2}+{1}^{2}}$,
QM=$\sqrt{(2\sqrt{2}-2)^{2}+{1}^{2}}$,
∴PM=PN=QN=QM,
∴四边形MPNQ是菱形,对角线的交点坐标为(5,5).
点评 本题考查二次函数综合题,待定系数法、二元二次方程组、两点之间的距离公式、菱形的判定等知识,解题的关键是灵活应用待定系数法确定函数解析式,学会利用方程组求两个函数图象的交点坐标,属于中考压轴题.

 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案| A. | -24÷22=-4 | B. | -22÷(-32)=$\frac{4}{27}$ | C. | -2×$\frac{1}{{3}^{2}}$=-8$\frac{1}{27}$ | D. | (-1)2016=1 |
| 试验次数 | 10 | 50 | 100 | 200 | 500 | 1000 | 2000 |
| 事件发生的 频率 | 0.245 | 0.248 | 0.251 | 0.253 | 0.249 | 0.252 | 0.251 |