题目内容
14.抛物线y=-$\frac{1}{2}$x2+bx+c与x轴分别交于点A(-2,0)、B(4,0),与y轴交于点C.(1)求抛物线解析式;
(2)求△CAB的面积.
分析 (1)将(-2,0),(4,0)代入函数解析式,列出b和c的二元一次方程组,求出b和c的值;
(2)首先求出点C的坐标,再求出AB的长,利用三角形面积公式求出答案即可.
解答 解:(1)将(-2,0),(4,0)代入函数解析式中得$\left\{\begin{array}{l}{-2-2b+c=0}\\{-8+4b+c=0}\end{array}\right.$,
解得:b=1,c=4.所以y=-$\frac{1}{2}$x2+x+4;
(2)当x=0时,y=4.所以C(0,4),AB=6.
S△ABC=$\frac{1}{2}$AB•OC=$\frac{1}{2}$×6×4=12.
点评 本题主要考查了抛物线与x轴的交点以及待定系数法求二次函数的解析式,解题的关键是列出b和c的二元一次方程组,此题难度不大.

练习册系列答案
相关题目
1.下列根式中与$\sqrt{2}$是同类二次根式的是( )
| A. | $\sqrt{24}$ | B. | $\sqrt{12}$ | C. | $\sqrt{18}$ | D. | $\sqrt{\frac{2}{3}}$ |
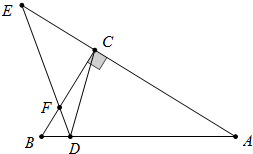 △ABC中,∠ACB=90°,AD=AC,∠CDE=45°,若BD=1,EF=2$\sqrt{5}$,则AD的长为4.
△ABC中,∠ACB=90°,AD=AC,∠CDE=45°,若BD=1,EF=2$\sqrt{5}$,则AD的长为4.
 如图,在△ABC中,∠ACB=90°,∠A=50°.将△ACD沿CD翻折,点A恰好落在BC边上的A′处,则∠A′DB=10°.
如图,在△ABC中,∠ACB=90°,∠A=50°.将△ACD沿CD翻折,点A恰好落在BC边上的A′处,则∠A′DB=10°.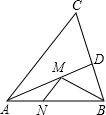 如图,在锐角△ABC中,AC=10,S△ABC=25,∠BAC的平分线交BC于点D,点M,N分别是AD和AB上的动点,则BM+MN的最小值是5.
如图,在锐角△ABC中,AC=10,S△ABC=25,∠BAC的平分线交BC于点D,点M,N分别是AD和AB上的动点,则BM+MN的最小值是5.