题目内容
 16、如图,将边长为2cm的正方形ABCD沿其对角线AC剪开,再把△ABC沿着BC平移得到△A′B′C′,设两三角形重叠部分的面积为S,则S的最大值为
16、如图,将边长为2cm的正方形ABCD沿其对角线AC剪开,再把△ABC沿着BC平移得到△A′B′C′,设两三角形重叠部分的面积为S,则S的最大值为2
cm2.分析:由平移性质可知,除去阴影部分的四个三角形仍能组成两个正方形,设B′C=x,则CC′=2-x,可以写出阴影部分的面积表达式,转化成二次函数求最值问题.
解答:解:∵△ABC沿着BC平移得到△A′B′C′,
∴除去阴影部分的四个三角形仍能组成两个正方形,
设B′C=x,则CC′=2-x,
阴影面积S=4-x2-(2-x)2=-(x-1)2+2,
当x=1,面积取到最大值,S=2,
故最大面积为2.
∴除去阴影部分的四个三角形仍能组成两个正方形,
设B′C=x,则CC′=2-x,
阴影面积S=4-x2-(2-x)2=-(x-1)2+2,
当x=1,面积取到最大值,S=2,
故最大面积为2.
点评:本题综合考查了图形的平移和二次函数求最值问题,是一道好题.

练习册系列答案
相关题目
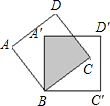 如图,将边长为2cm的两个正方形纸片完全重合,按住其中一个不动,另一个绕点B顺时针旋转一个角度,若使重叠部分的面积为
如图,将边长为2cm的两个正方形纸片完全重合,按住其中一个不动,另一个绕点B顺时针旋转一个角度,若使重叠部分的面积为4
| ||
| 3 |
| A、30° | B、35° |
| C、45° | D、60° |
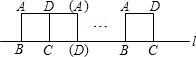 如图,将边长为2cm的正方形的四边沿直线l向右滚动(不滑动),当正方形滚动一周时,正方形的顶点A所经过的路线的长是
如图,将边长为2cm的正方形的四边沿直线l向右滚动(不滑动),当正方形滚动一周时,正方形的顶点A所经过的路线的长是
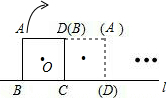 (2012•遵义)如图,将边长为
(2012•遵义)如图,将边长为 如图,将边长为2cm的两个互相重合的正方形纸片 按住其中一个不动,另一个纸点B顺时针旋转一个角度,若使重叠部分的面积为
如图,将边长为2cm的两个互相重合的正方形纸片 按住其中一个不动,另一个纸点B顺时针旋转一个角度,若使重叠部分的面积为