题目内容
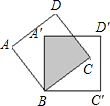如图，将边长为2cm的两个正方形纸片完全重合，按住其中一个不动，另一个绕点B顺时针旋转一个角度，若使重叠部分的面积为4
| ||
| 3 |
| A、30° | B、35° |
| C、45° | D、60° |
分析：根据旋转前后图形不变得出Rt△A′BM≌Rt△CBM，进而得出∠MBC的度数，从而得出∠CBC′的度数，即可得出答案．
解答：
解：连接BM，
在Rt△A′BM和Rt△CBM中，
∵
，
∴Rt△A′BM≌Rt△CBM（HL），
∵重叠部分的面积为
cm2，
∴Rt△A′BM与Rt△CBM面积相等为
cm2，
∴
×2×MC=
，
解得：MC=
，
∴tan∠MBC=
=
=
，
∴∠MBC=30°，
∴∠A′BM=30°，
∴∠CBC′=90°-30°×2=30°，
∴这个旋转角度为30°．
故选A．
解：连接BM，在Rt△A′BM和Rt△CBM中，
∵
|
∴Rt△A′BM≌Rt△CBM（HL），
∵重叠部分的面积为
4
| ||
| 3 |
∴Rt△A′BM与Rt△CBM面积相等为
2
| ||
| 3 |
∴
| 1 |
| 2 |
2
| ||
| 3 |
解得：MC=
2
| ||
| 3 |
∴tan∠MBC=
| MC |
| BC |
| ||||
| 2 |
| ||
| 3 |
∴∠MBC=30°，
∴∠A′BM=30°，
∴∠CBC′=90°-30°×2=30°，
∴这个旋转角度为30°．
故选A．
点评：此题主要考查了旋转的性质以及正方形的性质和全等三角形的判定，得出Rt△A′BM≌Rt△CBM是解决问题的关键．
练习册系列答案
相关题目
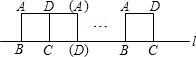如图，将边长为2cm的正方形的四边沿直线l向右滚动（不滑动），当正方形滚动一周时，正方形的顶点A所经过的路线的长是
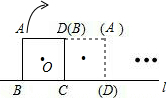（2012•遵义）如图，将边长为
如图，将边长为2cm的两个互相重合的正方形纸片 按住其中一个不动，另一个纸点B顺时针旋转一个角度，若使重叠部分的面积为