题目内容
 如图,将边长为2cm的两个互相重合的正方形纸片 按住其中一个不动,另一个纸点B顺时针旋转一个角度,若使重叠部分的面积为
如图,将边长为2cm的两个互相重合的正方形纸片 按住其中一个不动,另一个纸点B顺时针旋转一个角度,若使重叠部分的面积为4
| ||
| 3 |
30
30
度.分析:首先连接BE,得出Rt△A′BE≌Rt△CBE,进而得出S△A′BE=S△BCE=
×
=
,求出tan∠A′BE的值,即可得出旋转角,进而得出答案.
| 1 |
| 2 |
4
| ||
| 3 |
2
| ||
| 3 |
解答: 解:连接BE,
解:连接BE,
在Rt△A′BE和Rt△CBE中,
,
∴Rt△A′BE≌Rt△CBE(HL),
∴S△A′BE=S△BCE=
×
=
,
∵BC=A′B=2cm,
BC×EC=
A′B×A′E=
,
∴EC=A′E=
,
∴tan∠A′BE=
=
,
∴∠A′BE=∠EBC=30°,
∴∠A′BC=60°,
∴∠ABA′=90°-60°=30°,
则这个旋转角度为30度.
故答案为:30.
 解:连接BE,
解:连接BE,在Rt△A′BE和Rt△CBE中,
|
∴Rt△A′BE≌Rt△CBE(HL),
∴S△A′BE=S△BCE=
| 1 |
| 2 |
4
| ||
| 3 |
2
| ||
| 3 |
∵BC=A′B=2cm,
| 1 |
| 2 |
| 1 |
| 2 |
2
| ||
| 3 |
∴EC=A′E=
2
| ||
| 3 |
∴tan∠A′BE=
| ||||
| 2 |
| ||
| 3 |
∴∠A′BE=∠EBC=30°,
∴∠A′BC=60°,
∴∠ABA′=90°-60°=30°,
则这个旋转角度为30度.
故答案为:30.
点评:此题主要考查了旋转的性质以及锐角三角函数关系以及全等三角形的判定与性质等知识,根据已知得出S△A′BE=S△BCE是解题关键.

练习册系列答案
 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
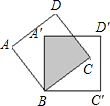 如图,将边长为2cm的两个正方形纸片完全重合,按住其中一个不动,另一个绕点B顺时针旋转一个角度,若使重叠部分的面积为
如图,将边长为2cm的两个正方形纸片完全重合,按住其中一个不动,另一个绕点B顺时针旋转一个角度,若使重叠部分的面积为4
| ||
| 3 |
| A、30° | B、35° |
| C、45° | D、60° |
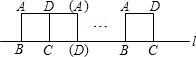 如图,将边长为2cm的正方形的四边沿直线l向右滚动(不滑动),当正方形滚动一周时,正方形的顶点A所经过的路线的长是
如图,将边长为2cm的正方形的四边沿直线l向右滚动(不滑动),当正方形滚动一周时,正方形的顶点A所经过的路线的长是
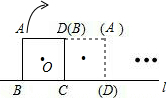 (2012•遵义)如图,将边长为
(2012•遵义)如图,将边长为