题目内容

（2012•遵义）如图，将边长为
2
cm的正方形ABCD沿直线l向右翻动（不滑动），当正方形连续翻动6次后，正方形的中心O经过的路线长是
3π
3π
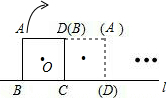
cm．（结果保留π）
分析：根据题意，画出正方形ABCD“滚动”时中心O所经过的轨迹，然后根据弧长的计算公式求得中心O所经过的路程．
解答：解：

∵正方形ABCD的边长为
2
cm，∴正方形的对角线长是2cm，翻动一次中心经过的路线的半径是以对角线的一半为半径，圆心角是90度的弧．
则中心经过的路线长是：
90π×1
180
×6=3πcm；
故答案是：3π．
点评：本题考查了弧长的计算、正方形的性质以及旋转的性质．在半径是R的圆中，因为360°的圆心角所对的弧长就等于圆周长C=2πR，所以n°圆心角所对的弧长为l=n°πR÷180°．
练习册系列答案
相关题目
（2012•遵义）如图，4张背面完全相同的纸牌（用①、②、③、④表示），在纸牌的正面分别写有四个不同的条件，小明将这4张纸牌背面朝上洗匀后，先随机摸出一张（不放回），再随机摸出一张．
（1）用树状图（或列表法）表示两次摸牌出现的所有可能结果；
（2）以两次摸出牌上的结果为条件，求能判断四边形ABCD是平行四边形的概率．
（2012•遵义）如图，△ABC是边长为6的等边三角形，P是AC边上一动点，由A向C运动（与A、C不重合），Q是CB延长线上一点，与点P同时以相同的速度由B向CB延长线方向运动（Q不与B重合），过P作PE⊥AB于E，连接PQ交AB于D．
（1）当∠BQD=30°时，求AP的长；
（2）当运动过程中线段ED的长是否发生变化？如果不变，求出线段ED的长；如果变化请说明理由．
（2012•遵义）如图，AB是⊙O的弦，AB长为8，P是⊙O上一个动点（不与A、B重合），过点O作OC⊥AP于点C，OD⊥PB于点D，则CD的长为
4
4
．
（2012•遵义）如图，△OAC中，以O为圆心，OA为半径作⊙O，作OB⊥OC交⊙O于B，垂足为O，连接AB交OC于点D，∠CAD=∠CDA．
（1）判断AC与⊙O的位置关系，并证明你的结论；
（2）若OA=5，OD=1，求线段AC的长．
（2012•遵义）如图，已知抛物线y=ax2+bx+c（a≠0）的图象经过原点O，交x轴于点A，其顶点B的坐标为（3，-
3
）．
（1）求抛物线的函数解析式及点A的坐标；
（2）在抛物线上求点P，使S△POA=2S△AOB；
（3）在抛物线上是否存在点Q，使△AQO与△AOB相似？如果存在，请求出Q点的坐标；如果不存在，请说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网