题目内容
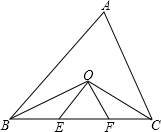 如图,△ABC中,∠ABC,∠ACB的平分线相交于点O,过点O作OE∥AB,OF∥AC,分别交BC于E,F,若BC=8cm,求△OEF的周长.
如图,△ABC中,∠ABC,∠ACB的平分线相交于点O,过点O作OE∥AB,OF∥AC,分别交BC于E,F,若BC=8cm,求△OEF的周长.考点:等腰三角形的判定与性质,平行线的性质
专题:
分析:由OB,OC分别是△ABC的∠ABC和∠ACB的平分线和OE∥AB、OF∥AC可推出BE=OE,OF=FC,显然△OEF的周长即为BC的长度.
解答:解:∵OB,OC分别是∠ABC,∠ACB的平分线,
∴∠ABO=∠EBO,∠ACO=∠FCO,
∵OE∥AB,OF∥AC,
∴∠ABO=∠BOE,∠ACO=∠COF,
∴∠EBO=∠BOE,∠FCO=∠COF,
∴BE=OE,OF=FC,
∴BC=BE+EF+FC=OF+OE+EF,
∵BC=8cm,
∴OF+OE+EF=8cm
∴△OEF的周长=OF+OE+EF=8cm.
∴∠ABO=∠EBO,∠ACO=∠FCO,
∵OE∥AB,OF∥AC,
∴∠ABO=∠BOE,∠ACO=∠COF,
∴∠EBO=∠BOE,∠FCO=∠COF,
∴BE=OE,OF=FC,
∴BC=BE+EF+FC=OF+OE+EF,
∵BC=8cm,
∴OF+OE+EF=8cm
∴△OEF的周长=OF+OE+EF=8cm.
点评:此题运用了平行线性质,角平分线定义以及等腰三角形的判定定理,较为灵活,难度中等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图折叠成一个正方体后和A面相对的是( )
如图折叠成一个正方体后和A面相对的是( )| A、B面 | B、D面 | C、E面 | D、F面 |
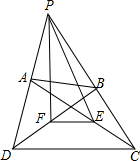 有四边形ABCD(任意),AD与BC的延长线交于D点,E、F分别为AC、BD的中点,连接EF、FP、EP,则S四边形ABCD=
有四边形ABCD(任意),AD与BC的延长线交于D点,E、F分别为AC、BD的中点,连接EF、FP、EP,则S四边形ABCD= 已知等腰△ABC中,AB=AC,AD⊥BC于D,CG∥AB,BG交AD、AC于E、F,连接EC,试说明:∠G=∠ACE.
已知等腰△ABC中,AB=AC,AD⊥BC于D,CG∥AB,BG交AD、AC于E、F,连接EC,试说明:∠G=∠ACE.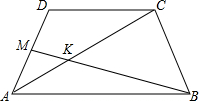 已知,如图,在梯形ABCD中,AB∥CD,M是AD中点,BM交AC于点K,AC=24cm,DC:AB=2:5,求AK、KC的长.
已知,如图,在梯形ABCD中,AB∥CD,M是AD中点,BM交AC于点K,AC=24cm,DC:AB=2:5,求AK、KC的长.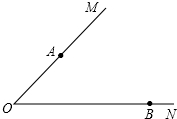 (1)先化简,再求值:
(1)先化简,再求值: 如图,AB=AC,D为BC上一点,DE⊥AB,DF⊥AC,BH⊥AC,求证:DE+DF=BH.
如图,AB=AC,D为BC上一点,DE⊥AB,DF⊥AC,BH⊥AC,求证:DE+DF=BH.