题目内容
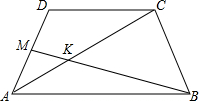 已知,如图,在梯形ABCD中,AB∥CD,M是AD中点,BM交AC于点K,AC=24cm,DC:AB=2:5,求AK、KC的长.
已知,如图,在梯形ABCD中,AB∥CD,M是AD中点,BM交AC于点K,AC=24cm,DC:AB=2:5,求AK、KC的长.考点:梯形,相似三角形的判定与性质
专题:
分析:设DC=2x,则AB=5x,过点M作MN∥CD交AC于点N,由M是AD中点可知MN是△ACD的中位线,故MN=
CD=x,AN=
AC=12cm,再由MN∥CD,CD∥AB可知MN∥AB,故可得出△MNK∽△BAK,再由相似三角形的对应边成比例可得出A的长,进而得出KC的长.
| 1 |
| 2 |
| 1 |
| 2 |
解答: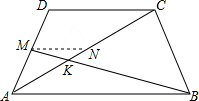 解:∵DC:AB=2:5,
解:∵DC:AB=2:5,
∴设DC=2x,则AB=5x.
过点M作MN∥CD交AC于点N,
∵M是AD中点,
∴MN是△ACD的中位线,
∴MN=
CD=x,AN=
AC=12cm.
∵MN∥CD,CD∥AB,
∴MN∥AB,
∴∠KBA=∠KMN,∠KAB=∠KNM,
∴△MNK∽△BAK,
∴
=
,即
=
,
解得AK=10,
∴KC=AC-AK=24-10=14(cm).
 解:∵DC:AB=2:5,
解:∵DC:AB=2:5,∴设DC=2x,则AB=5x.
过点M作MN∥CD交AC于点N,
∵M是AD中点,
∴MN是△ACD的中位线,
∴MN=
| 1 |
| 2 |
| 1 |
| 2 |
∵MN∥CD,CD∥AB,
∴MN∥AB,
∴∠KBA=∠KMN,∠KAB=∠KNM,
∴△MNK∽△BAK,
∴
| MN |
| AB |
| NK |
| AK |
| x |
| 5x |
| 12-AK |
| AK |
解得AK=10,
∴KC=AC-AK=24-10=14(cm).
点评:本题考查的是梯形,根据题意作出辅助线,构造出相似三角形是解答此题的关键.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
 如图,已知BE与CD相交于点A,M为BC的中点,∠1=∠2,AB=AC,求证:∠DBM=∠ECM.
如图,已知BE与CD相交于点A,M为BC的中点,∠1=∠2,AB=AC,求证:∠DBM=∠ECM.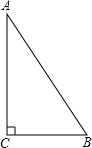 如图,在△ABC中,∠C=90°,∠A=30°,试通过折叠法证明∠A的对边BC是斜边AB的一半.
如图,在△ABC中,∠C=90°,∠A=30°,试通过折叠法证明∠A的对边BC是斜边AB的一半.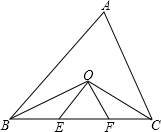 如图,△ABC中,∠ABC,∠ACB的平分线相交于点O,过点O作OE∥AB,OF∥AC,分别交BC于E,F,若BC=8cm,求△OEF的周长.
如图,△ABC中,∠ABC,∠ACB的平分线相交于点O,过点O作OE∥AB,OF∥AC,分别交BC于E,F,若BC=8cm,求△OEF的周长.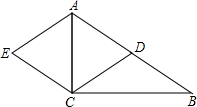 如图,在Rt△ABC中,∠ACB=90°,点D是斜边AB的中点,点A、C分别作AE∥CD,CE∥AB,CE、AE交于点E,求证:四边形ADCE是菱形.
如图,在Rt△ABC中,∠ACB=90°,点D是斜边AB的中点,点A、C分别作AE∥CD,CE∥AB,CE、AE交于点E,求证:四边形ADCE是菱形.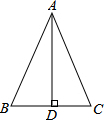 如图,已知△ABC中,AB=AC,AD⊥BC于点D,若△ABC、△ABD的周长分别为20cm、16cm,求AD的长.
如图,已知△ABC中,AB=AC,AD⊥BC于点D,若△ABC、△ABD的周长分别为20cm、16cm,求AD的长.