题目内容
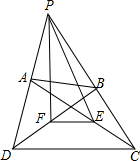 有四边形ABCD(任意),AD与BC的延长线交于D点,E、F分别为AC、BD的中点,连接EF、FP、EP,则S四边形ABCD=
有四边形ABCD(任意),AD与BC的延长线交于D点,E、F分别为AC、BD的中点,连接EF、FP、EP,则S四边形ABCD=考点:面积及等积变换
专题:
分析:由E为AC的中点可得到S△PCE=
S△PAC,S△FCE=
S△FAC.由F为BD的中点可得S△ADF=
S△ABD,S△CBF=
S△CBD,S△PBF=
S△PBD,S△CBF=
S△CBD.然后由S△PEF=S△PFC-S△PEC-S△FCE就可得到S△PEF与S四边形ABCD的关系,从而解决问题.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答: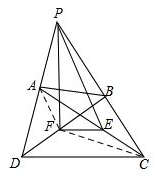 解:∵E为AC的中点,
解:∵E为AC的中点,
∴S△PAE=S△PCE=
S△PAC,S△FAE=S△FCE=
S△FAC.
∵F为BD的中点,
∴S△ADF=S△ABF=
S△ABD,S△CDF=S△CBF=
S△CBD,
S△PDF=S△PBF=
S△PBD,S△CDF=S△CBF=
S△CBD.
∴S△PEF=S△PFC-S△PEC-S△FCE
=S△PBF+S△CBF-S△PEC-S△FCE
=
S△PBD+
S△CBD-
S△PAC-
S△FAC
=
(S△PBD+S△CBD-S△PAC-S△FAC)
=
(S△AFD+S△CFD)
=
(
S△ADB+
S△CBD)
=
S四边形ABCD,
∴S四边形ABCD=4S△PEF.
故答案为:4.
 解:∵E为AC的中点,
解:∵E为AC的中点,∴S△PAE=S△PCE=
| 1 |
| 2 |
| 1 |
| 2 |
∵F为BD的中点,
∴S△ADF=S△ABF=
| 1 |
| 2 |
| 1 |
| 2 |
S△PDF=S△PBF=
| 1 |
| 2 |
| 1 |
| 2 |
∴S△PEF=S△PFC-S△PEC-S△FCE
=S△PBF+S△CBF-S△PEC-S△FCE
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
=
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 4 |
∴S四边形ABCD=4S△PEF.
故答案为:4.
点评:本题主要考查了等积变换,充分运用三角形的中线把三角形分成面积相等的两部分是解决本题的关键.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案
相关题目
在实数-3.14,
,π,
,
,0,
,0.1010010001…(每两个1之间的0的个数依次多1)中,无理数的个数是( )
| 2 |
| 3 | 64 |
| ||
| 3 |
| 9 |
| A、2个 | B、3个 | C、4个 | D、5个 |
2x2-3x+1=0用配方法解时正确的配方是( )
A、(x-
| ||||
B、(x-
| ||||
C、(x-
| ||||
D、(x+
|
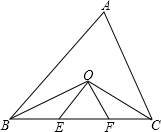 如图,△ABC中,∠ABC,∠ACB的平分线相交于点O,过点O作OE∥AB,OF∥AC,分别交BC于E,F,若BC=8cm,求△OEF的周长.
如图,△ABC中,∠ABC,∠ACB的平分线相交于点O,过点O作OE∥AB,OF∥AC,分别交BC于E,F,若BC=8cm,求△OEF的周长.